
【题目】已知二次函数![]() 的图像如图所示,对称轴是直线x=1,下列结论中:①abc>0,②2a+b=0,③
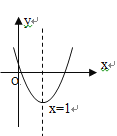
的图像如图所示,对称轴是直线x=1,下列结论中:①abc>0,②2a+b=0,③![]() <0,④4a+2b+c>0,其中正确的是( )
<0,④4a+2b+c>0,其中正确的是( )
A. ①②B. ①③C. ②③D. ②④
【答案】D
【解析】
由抛物线开口向上,得到a>0,再由对称轴在y轴右侧,得到a与b异号,可得出b<0,又抛物线与y轴正半轴相交,得到c>0,可得出abc<0,选项①错误;最后由对称轴为直线x=1,利用对称轴公式得到2a+b=0,选项②正确;由抛物线与x轴有2个交点,得到根的判别式b2-4ac大于0,故③错误;由x=2时对应的函数值>0,将x=2代入抛物线解析式可得出4a+2b+c大于0,得到选项④正确
∵抛物线的开口向上,∴a>0,
∵-![]() >0,∴b<0,
>0,∴b<0,
∵抛物线与y轴交于正半轴,∴c>0,
∴abc<0,①错误;
∵对称轴为直线x=1,∴-![]() =1,即2a+b=0,②正确,
=1,即2a+b=0,②正确,
∵抛物线与x轴有2个交点,∴b2-4ac>0,③错误;
∵对称轴为直线x=1,
∴x=2时,y>0,∴4a+2b+c>0,④正确;
所以正确的有②④.
故选:D.


科目:初中数学 来源: 题型:
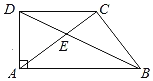
【题目】已知:如图,在梯形ABCD中,CD∥AB,∠DAB=90°,对角线AC、BD相交于点E,AC⊥BC,垂足为点C,且BC2=CECA.
(1)求证:AD=DE;
(2)过点D作AC的垂线,交AC于点F,求证:CE2=AEAF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数与反比例函数的图象交于点P(-2,1)和Q(1,m).
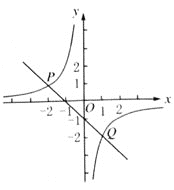
(1)求反比例函数的关系式;
(2)求Q点的坐标和一次函数的解析式;
(3)观察图象回答:当x为何值时,一次函数的值大于反比例函数的值?
查看答案和解析>>
科目:初中数学 来源: 题型:
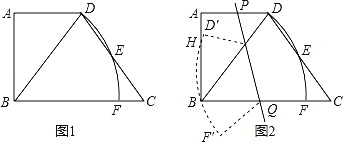
【题目】如图1,在梯形ABCD中,AD∥BC,∠ABC=90°,cosC=![]() ,DC=5,BC=6,以点B为圆心,BD为半径作圆弧,分别交边CD、BC于点E、F.
,DC=5,BC=6,以点B为圆心,BD为半径作圆弧,分别交边CD、BC于点E、F.
(1)求sin∠BDC的值;
(2)联结BE,设点G为射线DB上一动点,如果△ADG相似于△BEC,求DG的长;
(3)如图2,点P、Q分别为边AD、BC上动点,将扇形DBF沿着直线PQ折叠,折叠后的弧D'F'经过点B与AB上的一点H(点D、F分别对应点D',F'),设BH=x,BQ=y,求y关于x的函数关系式(不需要写定义域).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市某中学计划购进若干个甲种规格的排球和乙种规格的足球. 如果购买20个甲种规格的排球和15个乙种规格的足球,一共需要花费2050元; 如果购买10个甲种规格的排球和20个乙种规格的足球,一共需要花费1900元.
(1)求每个甲种规格的排球和每个乙种规格的足球的价格分别是多少元?
(2)如果学校要购买甲种规格的排球和乙种规格的足球共50个,并且预算总费用不超过3210元,那么该学校至多能购买多少个乙种规格的足球?
查看答案和解析>>
科目:初中数学 来源: 题型:
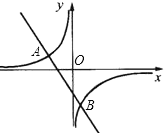
【题目】如图,一次函数y=kx+b的图象与反比例函数y=![]() 的图象交于A(﹣2,1),B(1,n)两点.
的图象交于A(﹣2,1),B(1,n)两点.
(1)求反比例函数和一次函数的解析式;
(2)根据图象写出使一次函数的值>反比例函数的值的x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,D是![]() 的中点,BC与AD,OD分别交于点E,F.
的中点,BC与AD,OD分别交于点E,F.
(1)求证:OD∥AC;
(2)求证:DC2=DEDA;
(3)若⊙O的直径AB=10,AC=6,求BF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
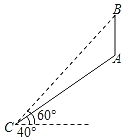
【题目】如图,在一坡角40°,坡面长AC=100m的小山顶上安装了一电信基站AB,在山底的C处,测得塔顶仰角为60°,求塔的高AB.(精确到0.1m)(以下供参考:sin40°≈0.64,cos40°≈0.77,tan40°≈0.84,![]() ≈1.73)
≈1.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在四边形ABCD中∠A=∠ABC=90°,点E是CD的中点,△ABD与 △EBD关于直线BD对称,![]() ,
,![]() .
.
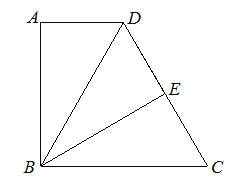
(1)求点A和点E之间的距离;
(2)联结AC交BE于点F,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com