
【题目】如图,AB为⊙O的直径,D是![]() 的中点,BC与AD,OD分别交于点E,F.
的中点,BC与AD,OD分别交于点E,F.
(1)求证:OD∥AC;
(2)求证:DC2=DEDA;
(3)若⊙O的直径AB=10,AC=6,求BF的长.

【答案】(1)见解析;(2)见解析;(3)4
【解析】
(1)由D是![]() 的中点,推出∠CAB=2∠BAD,再根据∠BOD=2∠BAD得∠CAB=∠BOD,故AC∥OD;
的中点,推出∠CAB=2∠BAD,再根据∠BOD=2∠BAD得∠CAB=∠BOD,故AC∥OD;
(2)证明△DCE∽△DCA,即可求解;
(3)根据△BOF∽△BAC,列出![]() =
=![]() ,求出BF=4.
,求出BF=4.
(1)因为点D是弧BC的中点,
所以∠CAD=∠BAD,即∠CAB=2∠BAD,
而∠BOD=2∠BAD,
所以∠CAB=∠BOD,
所以DO∥AC;
(2)∵D是![]() 的中点,
的中点,
∴∠CAD=∠DCB,
∴△DCE∽△DAC,
∴CD2=DEDA;
(3)∵AB为⊙O的直径
∴∠ACB=90°,
在Rt△ACB中,BC=.![]() =8,
=8,
∵OD∥AC,
∴△BOF∽△BAC,
∴![]() ,
,
即![]() =
=![]() ,
,
∴BF=4.
即BF的长为4.


 科学实验活动册系列答案
科学实验活动册系列答案科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,AC=6,BC=8,点D、E分别是边BC、AB上一点,DE∥AC,BD=5![]() ,把△BDE绕着点B旋转得到△BD'E'(点D、E分别与点D',E'对应),如果点A,D'、E'在同一直线上,那么AE'的长为_____.
,把△BDE绕着点B旋转得到△BD'E'(点D、E分别与点D',E'对应),如果点A,D'、E'在同一直线上,那么AE'的长为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
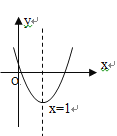
【题目】已知二次函数![]() 的图像如图所示,对称轴是直线x=1,下列结论中:①abc>0,②2a+b=0,③
的图像如图所示,对称轴是直线x=1,下列结论中:①abc>0,②2a+b=0,③![]() <0,④4a+2b+c>0,其中正确的是( )
<0,④4a+2b+c>0,其中正确的是( )
A. ①②B. ①③C. ②③D. ②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与
与![]() 轴相交于
轴相交于![]() 、
、![]() 两点,与
两点,与![]() 轴相交于点
轴相交于点![]() ,且点
,且点![]() 与点
与点![]() 的坐标分别为
的坐标分别为![]() .
.![]() ,点
,点![]() 是抛物线的顶点.点
是抛物线的顶点.点![]() 为线段
为线段![]() 上一个动点,过点
上一个动点,过点![]() 作
作![]() 轴于点
轴于点![]() ,若
,若![]() .
.
(1)求二次函数解析式;
(2)设![]() 的面积为
的面积为![]() ,试判断
,试判断![]() 有最大值或最小值?若有,求出其最值,若没有,请说明理由;
有最大值或最小值?若有,求出其最值,若没有,请说明理由;
(3)在![]() 上是否存在点
上是否存在点![]() ,使
,使![]() 为直角三角形?若存在,请写出点
为直角三角形?若存在,请写出点![]() 的坐标若不存在,请说明理由.
的坐标若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解高邮市“新冠肺炎”疫情防控期间九年级学生线上学习情况,通过问卷网就“你对自己线上学习的效果评价”进行了问卷调查,从中随机抽取了部分样卷进行统计,绘制了如下的统计图
根据统计图信息,解答下列问题:
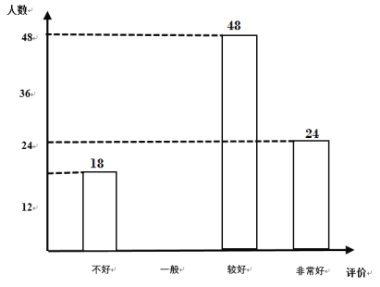
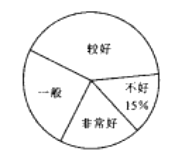
(1)本次调查的样本容量为 ;
(2)请补全条形统计图;
(3)扇形统计图中“较好”对应的扇形圆心角的度数为 ![]() ;
;
(4)若全市九年级线上学习人数有![]() 人,请估计对线上学习评价“非常好”的人数.
人,请估计对线上学习评价“非常好”的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
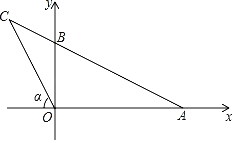
【题目】如图,在平面直角坐标系中,AB=3![]() ,连结AB并延长至C,连结OC,若满足OC2=BCAC,tanα=2,则点C的坐标为( )
,连结AB并延长至C,连结OC,若满足OC2=BCAC,tanα=2,则点C的坐标为( )
A.(﹣2,4)B.(﹣3,6)C.(﹣![]() ,
,![]() )D.(﹣
)D.(﹣![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 过A(-1,0)、B(3,0),直线AD交抛物线于点D,点D的横坐标为2,点P(m,n)是线段AD上的动点.
过A(-1,0)、B(3,0),直线AD交抛物线于点D,点D的横坐标为2,点P(m,n)是线段AD上的动点.
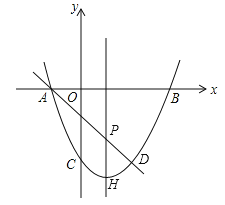
(1)求抛物线和直线AD的解析式;
(2)过点P的直线垂直于x轴,交抛物线于点H,
①求线段PH的长度l与m的关系式;
②当PH=2时,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
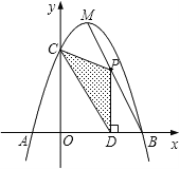
【题目】如图,已知抛物线y=ax2+bx+c(a≠0)与x轴交于点A、B,与y轴分别交于点C,其中点A(﹣1,0),OB=4OA,OC=2OA
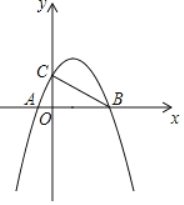
(1)求抛物线的解析式.
(2)点P是线段AB一动点,过P作PD∥AC交BC于D,当△PCD面积最大时,求点P的坐标.
(3)点M是位于线段BC上方的抛物线上一点,当∠ABC恰好等于△BCM中的某个角时,直接写出点M的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com