
【题目】如图,六边形![]() 是正六边形,点
是正六边形,点![]() 是边
是边![]() 的中点,
的中点,![]() 分别与
分别与![]() 交于点
交于点![]() ,则
,则![]() 四边形MCDN的值为( )
四边形MCDN的值为( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】A
【解析】
设BE的中点为O,则O为正六边形ABCDEF的中心,过点O作OQ⊥CD于Q,连接AC交BE于G,连接FD交BE于H,根据六边形![]() 是正六边形得到正六边形的边长都相等,各内角都相等,都等于120°,从而得到∠BAC=∠BCA=30°,∠AGB=∠CGB=∠FHB=∠DHE=90°,AG=CG,所以∠CAF=∠AFD=∠CDF=∠GCD=∠OGC=90°,根据直角三角形中30°所对的边等于斜边的一半,得到AB=2BG,可以得到四边形ACDF和四边形OGCQ都是矩形,所以AF∥GH∥CD,AF=GH=CD,OQ=CG=AG,设BG=a,则AB=2a,AP=
是正六边形得到正六边形的边长都相等,各内角都相等,都等于120°,从而得到∠BAC=∠BCA=30°,∠AGB=∠CGB=∠FHB=∠DHE=90°,AG=CG,所以∠CAF=∠AFD=∠CDF=∠GCD=∠OGC=90°,根据直角三角形中30°所对的边等于斜边的一半,得到AB=2BG,可以得到四边形ACDF和四边形OGCQ都是矩形,所以AF∥GH∥CD,AF=GH=CD,OQ=CG=AG,设BG=a,则AB=2a,AP=![]() AF=
AF=![]() AB=
AB=![]() ×2a=a,CD=AB=a,CD=AB=2a,GH=AF=2a,根据GM∥AP得到△CGM∽△CAP和△DHN∽△DFP,可得GM=
×2a=a,CD=AB=a,CD=AB=2a,GH=AF=2a,根据GM∥AP得到△CGM∽△CAP和△DHN∽△DFP,可得GM=![]() AP=
AP=![]() a,NH=
a,NH=![]() PF=
PF=![]() a,根据线段的和差可以求出BM,MN,AG,CD的长,根据三角形面积公式和梯形面积公式即可求出S△PBM和S四边形MCDN的面积,从而得到它们的比值.
a,根据线段的和差可以求出BM,MN,AG,CD的长,根据三角形面积公式和梯形面积公式即可求出S△PBM和S四边形MCDN的面积,从而得到它们的比值.
解:设BE的中点为O,则O为正六边形ABCDEF的中心,过点O作OQ⊥CD于Q,连接AC交BE于G,连接FD交BE于H,如图:
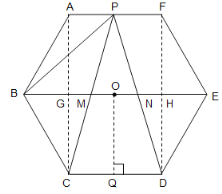
∵六边形ABCDEF是正六边形,P是AF的中点
∴∠ABC=∠BCD=∠CDE=∠DEF=∠EFA=∠BAF=120°,AB=BC=CD=DE=EF=AF,BE平分∠ABC,EB平分∠DEF,AP=PF
∴∠BAC=∠BCA=![]() =30°,∠AGB=∠CGB=∠FHB=∠DHE=90°,AG=CG
=30°,∠AGB=∠CGB=∠FHB=∠DHE=90°,AG=CG
∴AB=2BG,∠CAF=∠AFD=∠CDF=∠GCD=∠OGC=90°
∴四边形ACDF和四边形OGCQ都是矩形
∴AF∥GH∥CD,AF=GH=CD,OQ=CG=AG
设BG=a,则AB=2a
∴AP=![]() AF=
AF=![]() AB=
AB=![]() ×2a=a,CD=AB=a,CD=AB=2a,GH=AF=2a
×2a=a,CD=AB=a,CD=AB=2a,GH=AF=2a
∵GM∥AP
∴△CGM∽△CAP
∴![]()
∴GM=![]() AP=
AP=![]() a
a
同理可得NH=![]() PF=
PF=![]() a,
a,
∴BM=BG+GM=a+![]() a=
a=![]() a,MN=GH-GM-NH=2a-
a,MN=GH-GM-NH=2a-![]() a-
a-![]() a=a
a=a
在Rt△ABG中,AG=![]()
∴OQ=GC=AG=![]()
∴![]() =
=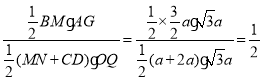
故选A.


科目:初中数学 来源: 题型:
【题目】关于x的方程(2m+1)x2+4mx+2m﹣3=0有两个不相等的实数根.
(1)求m的取值范围;
(2)是否存在实数m,使方程的两个实数根的倒数之和等于﹣1?若存在,求出m的值;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
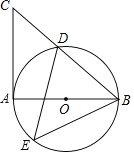
【题目】如图,AB为⊙O的直径,AC切⊙O于点A,连结BC交O于点D,E是⊙O上一点,且与点D在AB异侧,连结DE
(1)求证:∠C=∠BED;
(2)若∠C=50°,AB=2,则![]() 的长为(结果保留π)
的长为(结果保留π)
查看答案和解析>>
科目:初中数学 来源: 题型:
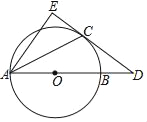
【题目】如图,点D在⊙O的直径AB的延长线上,CD切⊙O于点C,AE⊥CD于点E
(1)求证:AC平分∠DAE;
(2)若AB=6,BD=2,求CE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年由于防控疫情,师生居家隔离线上学习,AB和CD是社区两栋邻楼的示意图,小华站在自家阳台的C点,测得对面楼顶点A的仰角为30°,地面点E的俯角为45°.点E在线段BD上.测得B,E间距离为8.7米.楼AB高12![]() 米.求小华家阳台距地面高度CD的长(结果精确到1米,
米.求小华家阳台距地面高度CD的长(结果精确到1米,![]() 1.41,
1.41,![]() 1.73)
1.73)

查看答案和解析>>
科目:初中数学 来源: 题型:
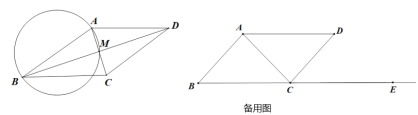
【题目】在![]() 中,
中,![]() 是锐角,过
是锐角,过![]() 两点以
两点以![]() 为半径作
为半径作![]()
(1)如图,对角线![]() 交于点
交于点![]() ,若
,若![]() ,且
,且![]() 过点
过点![]() ,求
,求![]() 的值
的值
(2)![]() 与边
与边![]() 的延长线交于点
的延长线交于点![]() ,
,![]() 的延长线交
的延长线交![]() 于点
于点![]() ,连接
,连接![]() ,若
,若![]() ,
,![]() 的长为
的长为![]() ,当
,当![]() 时,求
时,求![]() 的度数(提示:可再备用图上补全示意图)
的度数(提示:可再备用图上补全示意图)
查看答案和解析>>
科目:初中数学 来源: 题型:
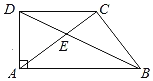
【题目】已知:如图,在梯形ABCD中,CD∥AB,∠DAB=90°,对角线AC、BD相交于点E,AC⊥BC,垂足为点C,且BC2=CECA.
(1)求证:AD=DE;
(2)过点D作AC的垂线,交AC于点F,求证:CE2=AEAF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工艺品厂生产一种汽车装饰品,每件生产成本为20元,销售价格在30元至80元之间(含30元和80元),销售过程中的管理、仓储、运输等各种费用(不含生产成本)总计50万元,其销售量y(万个)与销售价格(元/个)的函数关系如图所示.
(1)当30≤x≤60时,求y与x的函数关系式;
(2)求出该厂生产销售这种产品的纯利润w(万元)与销售价格x(元/个)的函数关系式;
(3)销售价格应定为多少元时,获得利润最大,最大利润是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在梯形ABCD中,AD∥BC,∠ABC=90°,cosC=![]() ,DC=5,BC=6,以点B为圆心,BD为半径作圆弧,分别交边CD、BC于点E、F.
,DC=5,BC=6,以点B为圆心,BD为半径作圆弧,分别交边CD、BC于点E、F.
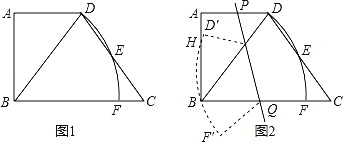
(1)求sin∠BDC的值;
(2)联结BE,设点G为射线DB上一动点,如果△ADG相似于△BEC,求DG的长;
(3)如图2,点P、Q分别为边AD、BC上动点,将扇形DBF沿着直线PQ折叠,折叠后的弧D'F'经过点B与AB上的一点H(点D、F分别对应点D',F'),设BH=x,BQ=y,求y关于x的函数关系式(不需要写定义域).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com