
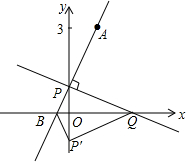
 如图,在平面直角坐标系中,O是坐标原点,点A的坐标是(1,3),点P的坐标是(0,b)(b>0且b≠3),直线AP交x轴于点B,过点P作PQ⊥AP,交x轴于点Q,点Q的坐标是(m,0),记点P关于x轴的对称点为P′,连接QP′、BP′.
如图,在平面直角坐标系中,O是坐标原点,点A的坐标是(1,3),点P的坐标是(0,b)(b>0且b≠3),直线AP交x轴于点B,过点P作PQ⊥AP,交x轴于点Q,点Q的坐标是(m,0),记点P关于x轴的对称点为P′,连接QP′、BP′.分析 (1)把点A,P的坐标代入直线的解析式,求得B的坐标即可求出结论.
(2)根据两直线垂直斜率的积等于-1,由直线AB的解析式求出直线PQ 的解析式即可得到结果.
(3)如图1,①当∠ABP′=90°时,得到∠PBO=∠P′BO=45°,根据等腰直角三角形的性质求出结论,②当∠AP′B=90°时,过点A作AM⊥y轴于M,根据三角形相似列比例式求得.
解答 解:(1)∵b=1,
∴P(0,1),
设直线AP的解析式为 y=kx+b,
∴$\left\{\begin{array}{l}{k+b=3}\\{b=1}\end{array}\right.$∴$\left\{\begin{array}{l}{k=2}\\{b=1}\end{array}\right.$,
∴直线AP的解析式为:y=2x+1,
∴B(-$\frac{1}{2}$,O),
∵点P关于x轴的对称点为P′,
∴PP′=2,
∴${S}_{△BPP′}=\frac{1}{2}$×$2×\frac{1}{2}$=$\frac{1}{2}$;
(2)设直线AB的解析式为:y=kx+b,
∴k+b=3,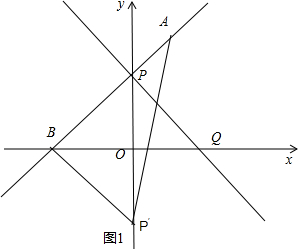
∴k=3-b,
∴直线AB的解析式为:y=(3-b)x+b,
∵PQ⊥AB,
∴直线PQ的解析式为:y=$\frac{1}{3-b}$x+b,
当y=0时,x=-b2+3b,
∴m=-b2+3b;
(3)如图1,①当∠ABP′=90°时,
∠PBO=∠P′BO=45°,
∴OB=$\frac{1}{2}$PP′,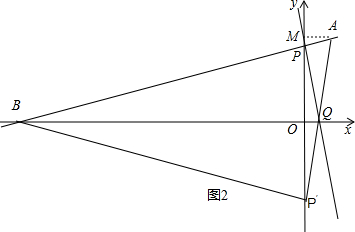
由(2)知,直线AB的解析式为:y=(3-b)x+b,
∴B(-$\frac{b}{3-b}$,0),p(0,b),
∴$\frac{b}{3-b}$=b,
∴b=2,
∴当b=m=2时,△ABP′为直角三角形,
②当∠AP′B=90°时,
过点A作AM⊥y轴于M,
则△AMP′∽△P′OB,
∴$\frac{AM}{P′O}$=$\frac{MP′}{BO}$,
∴$\frac{1}{b}$=$\frac{\frac{3+b}{b}}{3-b}$,
∴b2=8,∵b>0,∴b=2$\sqrt{2}$,
∴m=6$\sqrt{2}$-8.
点评 本题考查了待定系数法求函数的解析式,求三角形的面积,直角三角形的性质,相似三角形的判定和性质,正确的画出图形是解题的关键.


科目:初中数学 来源: 题型:选择题
| A. | 168(1+x)2=128 | B. | 168(1-x)2=128 | C. | 168(1-2x)2=128 | D. | 168(1-x2)=128 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
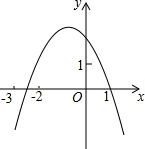 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列四个结论:①b<0;②c>1;③b2-4ac>0;④a-b+c<0;⑤a+b+1<0.其中正确的个数有( )
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列四个结论:①b<0;②c>1;③b2-4ac>0;④a-b+c<0;⑤a+b+1<0.其中正确的个数有( )| A. | 5个 | B. | 4个 | C. | 3个 | D. | 2个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 近似数6.95×105精确到千位 | B. | 3.14是有理数 | ||
| C. | -2$\sqrt{3}<-3\sqrt{2}$ | D. | π-3是无理数 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
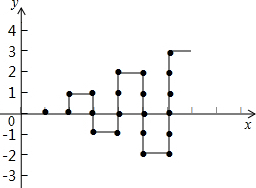
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,是抛物线y=ax2+bx+c(a≠0)图象的一部分.已知抛物线的对称轴为x=2,它与x轴的一个交点是(-1,0).则抛物线与x轴的另一个交点是(5,0);a+b+c<0(填“<或=或>”)
如图,是抛物线y=ax2+bx+c(a≠0)图象的一部分.已知抛物线的对称轴为x=2,它与x轴的一个交点是(-1,0).则抛物线与x轴的另一个交点是(5,0);a+b+c<0(填“<或=或>”)查看答案和解析>>
科目:初中数学 来源:2017届福建省仙游县郊尾、枫亭五校教研小片区九年级下学期第一次月考数学试卷(解析版) 题型:解答题
在平面直角坐标系中,动点P(x,y)满足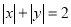 ,下图画出了符合条件的点P所组成图形的一部分,请将所有符合条件的点P所组成的图形补充完整.
,下图画出了符合条件的点P所组成图形的一部分,请将所有符合条件的点P所组成的图形补充完整.
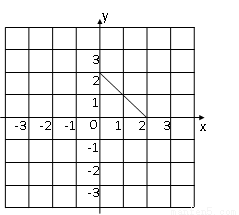
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com