
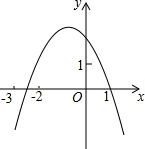 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列四个结论:①b<0;②c>1;③b2-4ac>0;④a-b+c<0;⑤a+b+1<0.其中正确的个数有( )
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列四个结论:①b<0;②c>1;③b2-4ac>0;④a-b+c<0;⑤a+b+1<0.其中正确的个数有( )| A. | 5个 | B. | 4个 | C. | 3个 | D. | 2个 |
分析 ①根据开口方向和对称轴,确定b的符号;
②根据抛物线与y轴的交点,确定c的符号;
③根据抛物线与x轴的交点情况,确定b2-4ac的符号;
④根据x=-1时,y>0,确定a-b+c的符号;
⑤根据x=1时,y=0,确定a+b+1的符号.
解答 解:①∵抛物线开口向下,a<0,对称轴在y轴左侧,
∴b<0,①正确;
②由抛物线与y轴的交点可知,c>1,②正确;
③抛物线与x轴的有两个交点,
∴b2-4ac>0,③正确;
④x=-1时,y>0,
∴a-b+c>0,④错误;
⑤x=1时,y=0,a+b+c=0,
∵c>1,
∴a+b+1<0,⑤正确,
故选:B.
点评 本题考查的是二次函数图象与系数的关系,根据开口方向、对称轴、与y轴的交点确定a、b、c的符号,根据抛物线与x轴的交点情况,确定b2-4ac的符号.


 智慧小复习系列答案
智慧小复习系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
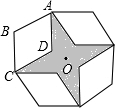 如图,是将菱形ABCD以点O为中心按顺时针方向分别旋转90°,180°,270°后形成的图形.若∠BAD=60°,AB=1,则图中阴影部分的面积为3-$\sqrt{3}$.
如图,是将菱形ABCD以点O为中心按顺时针方向分别旋转90°,180°,270°后形成的图形.若∠BAD=60°,AB=1,则图中阴影部分的面积为3-$\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
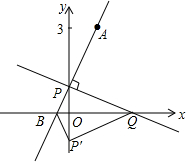 如图,在平面直角坐标系中,O是坐标原点,点A的坐标是(1,3),点P的坐标是(0,b)(b>0且b≠3),直线AP交x轴于点B,过点P作PQ⊥AP,交x轴于点Q,点Q的坐标是(m,0),记点P关于x轴的对称点为P′,连接QP′、BP′.
如图,在平面直角坐标系中,O是坐标原点,点A的坐标是(1,3),点P的坐标是(0,b)(b>0且b≠3),直线AP交x轴于点B,过点P作PQ⊥AP,交x轴于点Q,点Q的坐标是(m,0),记点P关于x轴的对称点为P′,连接QP′、BP′.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图是二次函数y=ax2+bx+c(a≠0)图象的一部分,直线x=-1是对称轴,有下列判断:①b-2a=0;②4a-2b+c<0;③a-b+c=-9a;④若(-3,y1),($\frac{3}{2}$,y2)是抛物线上两点,则y1>y2,其中正确的个数是( )
如图是二次函数y=ax2+bx+c(a≠0)图象的一部分,直线x=-1是对称轴,有下列判断:①b-2a=0;②4a-2b+c<0;③a-b+c=-9a;④若(-3,y1),($\frac{3}{2}$,y2)是抛物线上两点,则y1>y2,其中正确的个数是( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com