
分析 观察抛物线的解析式,它的开口向上,由于与x轴交于点A,B,得k>0,△ABP是等腰直角三角形,必须满足顶点坐标的纵坐标的绝对值与点A横坐标的绝对值相等,以此作为等量关系来列方程解出的值.
解答 解:∵抛物线解析式为y=x2-k,
∴该抛物线的顶点(0,-k),
∵抛物线和x轴有两个交点,
∴4k>0,
∴k>0,
令y=0,得x=±$\sqrt{k}$,
又∵抛物线y=x2-k与x轴的两个交点以及顶点围成的三角形是等腰直角三角形,
∴$\sqrt{k}$=k.
解得 k=1,
故答案为1.
点评 本题考查了抛物线与x轴的交点.此题利用“等腰直角三角形斜边上的中线等于斜边的一半”列出的等式.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
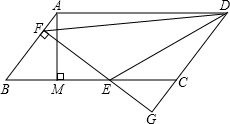 如图,平行四边形ABCD中,AB=5,BC=10,BC边上的高AM=4,E为BC边上一个动点(不与B,C重合),过E作直线AB的垂线,垂足为F,FE与DC的延长线相交于点G,连结DE,DF,当点E在线段BC上运动时,△BEF和△CEG的周长之和为( )
如图,平行四边形ABCD中,AB=5,BC=10,BC边上的高AM=4,E为BC边上一个动点(不与B,C重合),过E作直线AB的垂线,垂足为F,FE与DC的延长线相交于点G,连结DE,DF,当点E在线段BC上运动时,△BEF和△CEG的周长之和为( )| A. | 20 | B. | 24 | C. | 28 | D. | 36 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,ABCD是一张平行四边形纸片,要求利用所学知识作出一个菱形,甲、乙两位同学的作法如下:
如图,ABCD是一张平行四边形纸片,要求利用所学知识作出一个菱形,甲、乙两位同学的作法如下:| A. | 仅甲正确 | B. | 仅乙正确 | C. | 甲、乙均正确 | D. | 甲、乙均错误 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com