
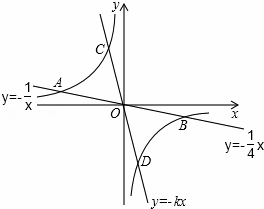
如图,已知双曲线y=﹣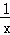 与两直线y=﹣
与两直线y=﹣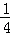 x,y=﹣kx(k>0,且k≠
x,y=﹣kx(k>0,且k≠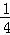 )分别相交于A、B、C、D四点.
)分别相交于A、B、C、D四点.
(1)当点C的坐标为(﹣1,1)时,A、B、D三点坐标分别是A( , ),B( , ),D( , ).
(2)证明:以点A、D、B、C为顶点的四边形是平行四边形.
(3)当k为何值时,▱ADBC是矩形.
考点: 反比例函数综合题;两点间的距离公式;一次函数的应用;平行四边形的判定与性质;矩形的判定.
专题: 综合题.
分析: (1)由C坐标,利用反比例函数的中心对称性确定出D坐标,联立双曲线y=﹣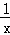 与直线y=﹣
与直线y=﹣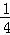 x,求出A与B坐标即可;
x,求出A与B坐标即可;
(2)由反比例函数为中心对称图形,利用中心对称性质得到OA=OB,OC=OD,利用对角线互相平分的四边形为平行四边形即可得证;
(3)由A与B坐标,利用两点间的距离公式求出AB的长,联立双曲线y=﹣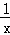 与直线y=﹣kx,表示出CD的长,根据对角线相等的平行四边形为矩形,得到AB=CD,即可求出此时k的值.
与直线y=﹣kx,表示出CD的长,根据对角线相等的平行四边形为矩形,得到AB=CD,即可求出此时k的值.
解答: 解:(1)∵C(﹣1,1),C,D为双曲线y=﹣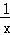 与直线y=﹣kx的两个交点,且双曲线y=﹣
与直线y=﹣kx的两个交点,且双曲线y=﹣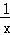 为中心对称图形,
为中心对称图形,
∴D(1,﹣1),
联立得: ,
,
消去y得:﹣ x=﹣
x=﹣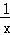 ,即x2=4,
,即x2=4,
解得:x=2或x=﹣2,
当x=2时,y=﹣ ;当x=﹣2时,y=
;当x=﹣2时,y= ,
,
∴A(﹣2, ),B(2,﹣
),B(2,﹣ );
);
故答案为:﹣2, ,2,﹣
,2,﹣ ,1,﹣1;
,1,﹣1;
(2)∵双曲线y=﹣ 为中心对称图形,且双曲线y=﹣
为中心对称图形,且双曲线y=﹣ 与两直线y=﹣
与两直线y=﹣ x,y=﹣kx(k>0,且k≠
x,y=﹣kx(k>0,且k≠ )分别相交于A、B、C、D四点,
)分别相交于A、B、C、D四点,
∴OA=OB,OC=OD,
则以点A、D、B、C为顶点的四边形是平行四边形;
(3)若▱ADBC是矩形,可得AB=CD,
联立得: ,
,
消去y得:﹣ =﹣kx,即x2=
=﹣kx,即x2=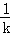 ,
,
解得:x=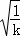 或x=﹣
或x=﹣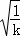 ,
,
当x=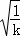 时,y=﹣
时,y=﹣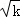 ;当x=﹣
;当x=﹣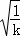 时,y=
时,y=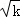 ,
,
∴C(﹣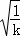 ,
,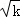 ),D(
),D( ,﹣
,﹣ ),
),
∴CD=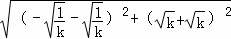 =AB=
=AB= =
=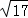 ,
,
整理得:(4k﹣1)(k﹣4)=0,
k1=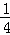 ,k2=4,
,k2=4,
又∵k≠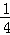 ,∴k=4,
,∴k=4,
则当k=4时,▱ADBC是矩形.
点评: 此题属于反比例函数综合题,涉及的知识有:坐标与图形性质,一次函数与反比例函数的交点,平行四边形,矩形的判定,两点间的距离公式,以及中心图形性质,熟练掌握性质是解本题的关键.


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:初中数学 来源: 题型:
如图,PA为⊙O的切线,点A为切点,直线PO交⊙O于点E,F,过点A作PO的垂线AB,垂足为点C,交⊙O于点B,延长BO与⊙O交于点D,连接AD,连接BE,
(1)求证: 直线PB为⊙O的切线,
直线PB为⊙O的切线,
(2)试探究线段EF,OP,OC之间的数量关系,并加以证明,
(3)若BC=9,tan∠E=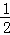 ,求cos∠ADB的值和线段PE的长.
,求cos∠ADB的值和线段PE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
如图,某天早晨王老师沿⊙M的半圆形M→A→B→M路径匀速散步,此时王老师离出发点M的距离y与时间x之间的函数关系的大致图象是( )
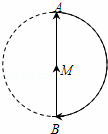
A.  B.
B. 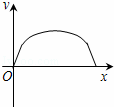 C.
C. 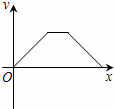 D.
D. 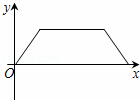
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,等边三角形ABC中,AB=3,点D,E分别在AB,AC上,且DE∥BC,沿直线DE折叠△ABC,当点A的对应点A′与△ABC的中心O重合时,折痕DE的长为 .
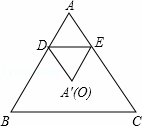
查看答案和解析>>
科目:初中数学 来源: 题型:
把下列各数填在相应的表示集合的大括号里:
﹣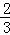 ,12,﹣(﹣96),﹣|﹣3|,﹣4.5,0,|﹣2.5|,
,12,﹣(﹣96),﹣|﹣3|,﹣4.5,0,|﹣2.5|,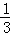
(1)正整数集合{ …}
(2)整数集合 { …}
(3)正分数集合{ …}
(4)负分数集合{ …}.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com