
 如图:已知P是半径为5cm的⊙O内一点.解答下列问题:
如图:已知P是半径为5cm的⊙O内一点.解答下列问题: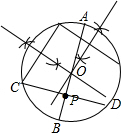 ;
;| 1 |
| 2 |
| 1 |
| 2 |


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
| 3 |
| 4 |
| 1 |
| 6 |
| 5 |
| 4 |
| 1 |
| 2 |
| 5 |
| 9 |
| 7 |
| 12 |
| 1 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 时间 | 第一个月 | 第二个月 | 清仓时 |
| 单价(元) | 80 | 40 | |
| 销量(件) | 200 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,一个质地均匀的正四面体(四个面都是正三角形),四个面上分别标有数字1、2、3、4.若连续投掷这个四面体两次,试用适当的方法求出下列各事件的概率.
如图,一个质地均匀的正四面体(四个面都是正三角形),四个面上分别标有数字1、2、3、4.若连续投掷这个四面体两次,试用适当的方法求出下列各事件的概率.查看答案和解析>>
科目:初中数学 来源: 题型:
| 1 |
| 5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com