练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
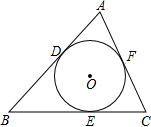
    3．如图，⊙O是△ABC的内切圆，点D、E、F为切点，AD=13，AC=25，BC=35，求BD的长度．

    分析 设BD=xcm，由于⊙O是△ABC的内切圆，则根据切线长定理得到AD=AF=13，BD=BE=x，CE=CF，然后利用CE=BC-BE=35-x，CF=AC-AF=12得到35-x=12，再解方程求出x即可．

    解答 解：设BD=xcm，
    ∵⊙O是△ABC的内切圆，点D、E、F为切点，
    ∴AD=AF=13，BD=BE=x，CE=CF，
    而CE=BC-BE=35-x，CF=AC-AF=25-13=12，
    ∴35-x=12，
    解得x=23，
    即BD的长为23cm．

    点评 本题考查了三角形的内切圆与内心：与三角形各边都相切的圆叫三角形的内切圆，三角形的内切圆的圆心叫做三角形的内心，这个三角形叫做圆的外切三角形．三角形的内心就是三角形三个内角角平分线的交点．也考查了切线长定理．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

    6．已知x2=16，那么x=±4；如果（-a）2=（-5）2，那么a=±5．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    7．如图，在△ABC中，若D、E分别是AB、AC上的点，且DE∥BC，AD=1，BD=2，则DE：BC=1：3．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    4．如图，已知线段AC，BD相交于点O，且OA=OC，OB=OD，E，F分别为DO，BO上两点，DE=BF，CE=9，求AF的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    11．如图所示，∠1=∠2，CD⊥AD，CB⊥AB．CD=CB，AC、EF相交于点G．求证：AC垂直平分EF．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

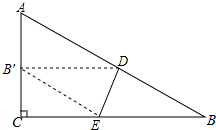    8．如图是一张直角三角形纸片，∠C=90°，点D在边AB上，若将三角形纸片沿直线DE折叠，使点B落在AC边上，记作点B′，连接B′E．
    （1）若DB′∥BC，求证：B′E∥AB．
    （2）点D是否是AB边的中点？如果是，请你证明你的结论，如果不是，说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

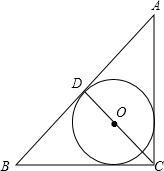    15．在Rt△ABC中，CD是斜边AB上的高，则图中的三个直角三角形（△ABC、△ACD、△BCD）的内切圆半径的和等于（　　）
    A．CDB．BCC．ACD．AB

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    12．如果不等式组$\left\{{\begin{array}{l}{x＜3}\\{x＞m}\end{array}}\right.$无解，那么m的取值范围是（　　）
    A．m≤3B．m≥3C．m＞3D．m＜3

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

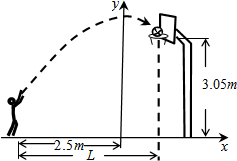    13．李老师在某次投篮中，球的运动路线是抛物线$y=-\frac{1}{5}{x^2}+3.5$的一部分，其相关数据如图所示，若命中篮圈中心，则他与蓝底的距离L为4米；若身高为1.79米的李老师是跳投命中篮圈中心的，且篮球在离李老师的头顶上方0.25米处出手，那么跳投时他跳离地面的高度为0.21米．

    查看答案和解析>>

    同步练习册答案