
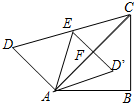
 如图,将一副直角三角板拼在一起得四边形ABCD,∠ACB=45°,∠ACD=30°,点E为CD边上的中点,连接AE,将△ADE沿AE所在直线翻折得到△AD′E,D′E交AC于F点,若AB=$6\sqrt{2}$cm,点D′到BC的距离是( )
如图,将一副直角三角板拼在一起得四边形ABCD,∠ACB=45°,∠ACD=30°,点E为CD边上的中点,连接AE,将△ADE沿AE所在直线翻折得到△AD′E,D′E交AC于F点,若AB=$6\sqrt{2}$cm,点D′到BC的距离是( )| A. | $3+\sqrt{3}$ | B. | $3\sqrt{2}+\sqrt{6}$ | C. | $3\sqrt{2}-\sqrt{6}$ | D. | $3-\sqrt{3}$ |
分析 连接CD′,BD′,过点D′作D′G⊥BC于点G,进而得出△ABD′≌△CBD′,于是得到∠D′BG=45°,D′G=GB,进而利用勾股定理求出点D′到BC边的距离.
解答 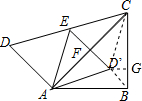 解:连接CD′,BD′,过点D′作D′G⊥BC于点G,
解:连接CD′,BD′,过点D′作D′G⊥BC于点G,
∵AC垂直平分线ED′,
∴AE=AD′,CE=CD′,
∵AE=EC,∴AD′=CD′=4$\sqrt{3}$,
在△ABD′和△CBD′中,
$\left\{\begin{array}{l}{AB=BC}\\{BD′=BD′}\\{AD′=CD′}\end{array}\right.$,
∴△ABD′≌△CBD′(SSS),
∴∠D′BG=45°,
∴D′G=GB,
设D′G长为xcm,则CG长为(6$\sqrt{2}$-x)cm,
在Rt△GD′C中
x2+(6$\sqrt{2}$-x)2=(4$\sqrt{3}$)2,
解得:x1=3$\sqrt{2}$-$\sqrt{6}$,x2=3$\sqrt{2}$+$\sqrt{6}$(舍去),
∴点D′到BC边的距离为(3$\sqrt{2}$-$\sqrt{6}$)cm.
故选C.
点评 此题主要考查了折叠的性质,全等三角形的判定与性质和锐角三角函数关系以及等边三角形的判定与性质等知识,利用垂直平分线的性质得出点E,D′关于直线AC对称是解题关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
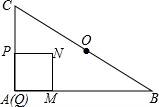 如图,在Rt△ABC中,AB=4,AC=3,点O为BC的中点,点P从点A出发,沿折线AC-CO以每秒1个单位长度的速度向终点O运动,当点P与点A不重合时,过点P作PQ⊥AB于点Q,以PQ为边向右作正方形PQMN,设正方形PQMN与Rt△ABC重叠部分图形的面积为S(平方单位),点P运动的时间为t(秒).
如图,在Rt△ABC中,AB=4,AC=3,点O为BC的中点,点P从点A出发,沿折线AC-CO以每秒1个单位长度的速度向终点O运动,当点P与点A不重合时,过点P作PQ⊥AB于点Q,以PQ为边向右作正方形PQMN,设正方形PQMN与Rt△ABC重叠部分图形的面积为S(平方单位),点P运动的时间为t(秒).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com