
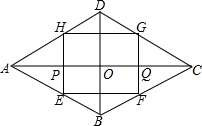
 ��ͼ��������ABCD�У������Խ��߳���AC=10��BD=6��F���߶�AO��һ�㣨����A��O�غϣ���Q���߶�OC��һ�㣬��AP=CQ���ֱ�BAD�͡�BCD�۵���ʹA��C���㶼�ڶԽ���AC�ϣ��ۺ۷ֱ���EH��FG��EH��P�㣬FG��Q�㣬����EF��HG���ٰ��۵�������ƽ��
��ͼ��������ABCD�У������Խ��߳���AC=10��BD=6��F���߶�AO��һ�㣨����A��O�غϣ���Q���߶�OC��һ�㣬��AP=CQ���ֱ�BAD�͡�BCD�۵���ʹA��C���㶼�ڶԽ���AC�ϣ��ۺ۷ֱ���EH��FG��EH��P�㣬FG��Q�㣬����EF��HG���ٰ��۵�������ƽ������ ��1���������ε����ʵõ���HAP=��EAP=��GCQ=��FCQ�����۵������ʵõ�AP��HE��CQ��GF���Ƴ���APH�ա�CQG���õ�PH=GQ��ͬ��PH=GQ=PE=FQ��֤���ı���EFGH��ƽ���ı��Σ��õ�HG��EF������ƽ���ߵ����ʵõ���AHF=��ADB����HAP=��DHG�����ɵõ����ۣ�
��2���������ε����ʵõ�AO=CO=$\frac{1}{2}$AC=5��AC��BD�����۵������ʵ�HE��BD���Ƴ���AEH�ס�ABD���õ�$\frac{HE}{BD}=\frac{AP}{AO}$�����HE=$\frac{6}{5}$x�����ݾ��ε������ʽ�õ�y=HE•PQ=$\frac{6}{5}$x•��10-2x�������ǵõ����ۣ��ڸ��������ε������з��̵õ�x=$\frac{25}{8}$�����ɵõ������
��� �⣺��1���ı���EFGH����״�Ǿ��Σ�
��������ABCD��
���HAP=��EAP=��GCQ=��FCQ��
���۵������ʵã�AP��HE��CQ��GF��
�ڡ�APH���CQG�У�
$\left\{\begin{array}{l}{��HAP=��GCQ}\\{��APH=��CQG=90��}\\{AP=CQ}\end{array}\right.$��
���APH�ա�CQG��
��PH=GQ��
ͬ��PH=GQ=PE=FQ��
��HE=GF��
��HE��GF��
���ı���EFGH��ƽ���ı��Σ�
��HG��EF��
���AHF=��ADB����HAP=��DHG��
�ߡ�HAP+��AHP=90�㣬
���AHP+��DHG=90�㣬
���EHG=90�㣬
���ı���EFGH�Ǿ��Σ�
�ʴ�Ϊ�����Σ�
��2���١�������ABCD�У�
��AO=CO=$\frac{1}{2}$AC=5��AC��BD��
���۵������ʵ�HE��BD��
��HE��BD��
���AEH�ס�ABD��
��$\frac{HE}{BD}=\frac{AP}{AO}$��
��$\frac{HE}{6}=\frac{x}{5}$��
��HE=$\frac{6}{5}$x��
��PQ=10-2x��
��y=HE•PQ=$\frac{6}{5}$x•��10-2x����
��y=-$\frac{12}{5}$x2+12x����0��y��15����
�ڵ��ı���EFGH��������ʱ����HE=EF��
��$\frac{6}{5}$x=10-2x��
��ã�x=$\frac{25}{8}$��
��y=-$\frac{12}{5}$x2+12x=$\frac{225}{16}$��
���� ���⿼�������ε����ʣ����ε��ж������ʣ������ε����ʣ�ȫ�������ε��ж������ʣ��۵������ʣ�����κ����Ľ���ʽ���������ո����ʶ����ǽ���Ĺؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��4x+y���� | B�� | ��4x-y���� | C�� | ��4x+5y���� | D�� | ��4x+9y���� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
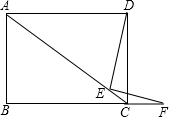 ��ͼ���ı���ABCDΪ���Σ�E�ڶԽ���AC�ϣ�F�ڱ�BC���ӳ����ϣ���$\frac{DE}{EF}$=$\frac{BC}{AB}$����֤��DE��EF��
��ͼ���ı���ABCDΪ���Σ�E�ڶԽ���AC�ϣ�F�ڱ�BC���ӳ����ϣ���$\frac{DE}{EF}$=$\frac{BC}{AB}$����֤��DE��EF���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��֪����y=-x2-2x+3��
��֪����y=-x2-2x+3���鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com