
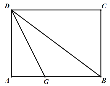
【题目】如图,折叠长方形纸片ABCD,先折出折痕(对角线)BD,再折叠使AD边与BD重合,得折痕DG,若AB=8,BC=6,则AG的长为____________ .
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,对角线AC、BD相交于点O,过点D作对角线BD的垂线交BA的延长线于点E.

(1)证明:四边形ACDE是平行四边形;
(2)若AC=8,BD=6,求△ADE的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A.“三角形任意两边之差小于第三边”是必然事件
B.在连续5次的测试中,两名同学的平均分相同,方差较大的同学成绩更稳定
C.某同学连续10次抛掷质量均匀的硬币,6次正面向上,因此正面向上的概率是60%
D.检测某品牌笔芯的使用寿命,适宜用普查
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在![]() 中,点
中,点![]() 分别在
分别在![]() 上,且
上,且![]() .设
.设![]() 的边
的边![]() 上的高为
上的高为![]() ,
,![]() 的边
的边![]() 上的高为
上的高为![]() .
.
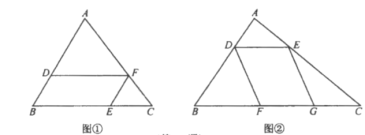
(1)若![]() 、
、![]() 的面积分别为3,1,则
的面积分别为3,1,则![]() ;
;
(2)设![]() 、
、![]() 、四边形
、四边形![]() 的面积分别为
的面积分别为![]() ,求证:
,求证:![]() ;
;
(3)如图②,在![]() 中,点
中,点![]() 分别在
分别在![]() 上,点
上,点![]() 在
在![]() 上,且
上,且![]() ,
, ![]() . 若
. 若![]() 、
、![]() 、
、![]() 的面积分别为3, 7, 5,求
的面积分别为3, 7, 5,求![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
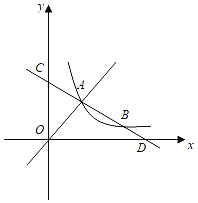
【题目】如图,直线CD分别与x轴、y轴交于点D,C,点A,B为线段CD的三等分点,且A,B在反比例函数y=![]() 的图象上,S△AOD=6.
的图象上,S△AOD=6.
(1)求k的值;
(2)若直线OA的表达式为y=2x,求点A的坐标;
(3)若点P在x轴上,且S△AOP=2S△BOD,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
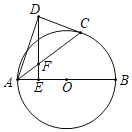
【题目】如图,AB是⊙O的直径,点C在半圆上,点D在圆外,DE⊥AB于点E交AC于点F,且DF=CD
(1)求证:CD是⊙O的切线;
(2)若点F是AC的中点,DF=2EF=2![]() ,求⊙O半径.
,求⊙O半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,P是AB边上的任意一点,过P点作PE⊥AB,交AD于E,连结CE、CP.已知∠A=60o .
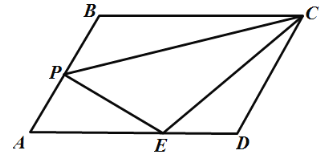
(1)试探究,当△CPE≌△CPB时,CD与DE的数量关系;
(2)若BC=4,AB=3,当AP的长为多少时,△CPE的面积最大,并求出面积的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
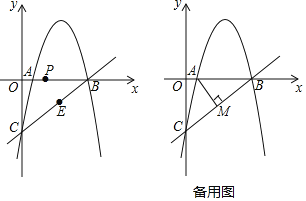
【题目】如图,抛物线![]() 经过x轴上的点A(1,0)和点B及y轴上的点C,经过B、C两点的直线为
经过x轴上的点A(1,0)和点B及y轴上的点C,经过B、C两点的直线为![]() .
.
①求抛物线的解析式.
②点P从A出发,在线段AB上以每秒1个单位的速度向B运动,同时点E从B出发,在线段BC上以每秒2个单位的速度向C运动.当其中一个点到达终点时,另一点也停止运动.设运动时间为t秒,求t为何值时,△PBE的面积最大并求出最大值.
③过点A作![]() 于点M,过抛物线上一动点N(不与点B、C重合)作直线AM的平行线交直线BC于点Q.若点A、M、N、Q为顶点的四边形是平行四边形,求点N的横坐标.
于点M,过抛物线上一动点N(不与点B、C重合)作直线AM的平行线交直线BC于点Q.若点A、M、N、Q为顶点的四边形是平行四边形,求点N的横坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
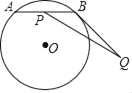
【题目】如图,⊙O上有一个动点A和一个定点B,令线段AB的中点是点P,过点B作⊙O的切线BQ,且BQ=3,现测得![]() 的长度是
的长度是![]() ,
,![]() 的度数是120°,若线段PQ的最大值是m,最小值是n,则mn的值是( )
的度数是120°,若线段PQ的最大值是m,最小值是n,则mn的值是( )
A. 3![]() B. 2
B. 2![]() C. 9 D. 10
C. 9 D. 10
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com