
【题目】梧州市特产批发市场有龟苓膏粉批发,其中A品牌的批发价是每包20元,B品牌的批发价是每包25元,小王需购买A、B两种品牌的龟苓膏共1000包.
(1)若小王按需购买A、B两种品牌龟苓膏粉共用22000元,则各购买多少包?
(2)凭会员卡在此批发市场购买商品可以获得8折优惠,会员卡费用为500元.若小王购买会员卡并用此卡按需购买1000包龟苓膏粉,共用了y元,设A品牌买了x包,请求出y与x之间的函数关系式.
(3)在(2)中,小王共用了20000元,他计划在网店包邮销售这批龟苓膏粉,每包龟苓膏粉小王需支付邮费8元,若每包销售价格A品牌比B品牌少5元,请你帮他计算,A品牌的龟苓膏粉每包定价不低于多少元时才不亏本(运算结果取整数)?
【答案】(1)A 600包、B 400包;(2)y=﹣4x+20500;(3)24.
【解析】
试题分析:(1)设小王需购买A、B两种品牌龟苓膏粉分别为x包、y包,根据题意列方程解出即可;
(2)根据题意,可得y=500+0.8×[20x+25(1000﹣x)],据此求出y与x之间的函数关系式即可.
(3)先求出小王购买A、B两种品牌龟苓膏粉分别为多少包,然后设A种品牌龟苓膏粉的售价为z元,则B种品牌龟苓膏粉的售价为z+5元,所以125z+875(z+5)≥20000+8×1000,据此求出A品牌的龟苓膏粉每包定价不低于多少元时才不亏本即可.
试题解析:(1)设小王需购买A、B两种品牌龟苓膏粉分别为x包、y包,则![]() ,解得:
,解得:![]() ,∴小王购买A、B两种品牌龟苓膏粉分别为600包、400包;
,∴小王购买A、B两种品牌龟苓膏粉分别为600包、400包;
(2)y=500+0.8×[20x+25(1000﹣x)]=500+0.8×[25000﹣5x]=500+20000﹣4x=﹣4x+20500,∴y与x之间的函数关系式是:y=﹣4x+20500;
(3)由(2),可得:20000=﹣4x+20500,解得x=125,∴小王购买A、B两种品牌龟苓膏粉分别为125包、875包,设A种品牌龟苓膏粉的售价为z元,则B种品牌龟苓膏粉的售价为z+5元,∴125z+875(z+5)≥20000+8×1000,解得z≥23.625,∴A品牌的龟苓膏粉每包定价不低于24元时才不亏本.


科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是正方形,BE⊥BF,BE=BF,EF与BC交于点G.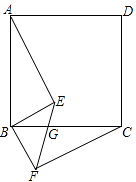
(1)求证:AE=CF;
(2)若∠ABE=65°,求∠EGC的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为培养学生养成良好的“爱读书,读好书,好读书”的习惯,我市某中学举办了“汉字听写大赛”,准备为获奖同学颁奖.在购买奖品时发现,一个书包和一本词典会花去48元,用124元恰好可以购买3个书包和2本词典.
(1)每个书包和每本词典的价格各是多少元?
(2)学校计划用总费用不超过900元的钱数,为获胜的40名同学颁发奖品(每人一个书包或一本词典),求最多可以购买多少个书包?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了绿化环境,育英中学八年级三班同学都积极参加植树活动,今年植树节时,该班同学植树情况的部分数据如图所示,请根据统计图信息,回答下列问题:(第(1),(3)小题需列式解答)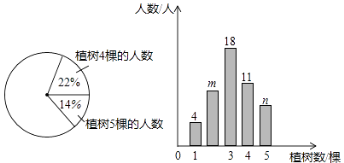
(1)八牛级三班共有多少名同学?
(2)条形统计图中,m= , n=。
(3)扇形统计图中,算出植树2棵的人数所对应的扇形圆心角的度数。
查看答案和解析>>
科目:初中数学 来源: 题型:
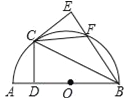
【题目】如图,以AB为直径作半圆O,点C为半圆上与A,B不重合的一动点,过点C作CD⊥AB于点D,点E与点D关于BC对称,BE与半圆交于点F,连CE.
(1)判断CE与半圆O的位置关系,并给予证明.
(2)点C在运动时,四边形OCFB的形状可变为菱形吗?若可以,猜想此时∠AOC的大小,并证明你的结论;若不可以,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:三角形ABC中,∠A=90°,AB=AC,D为BC的中点, 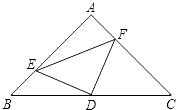
(1)如图,E,F分别是AB,AC上的点,且BE=AF,求证:△DEF为等腰直角三角形;
(2)若E,F分别为AB,CA延长线上的点,仍有BE=AF,其他条件不变,那么,△DEF是否仍为等腰直角三角形?证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】Rt△ABC中,∠C=90°,点D、E是△ABC边AC、BC上的点,点P是一动点.令∠PDA=∠1,∠PEB=∠2,∠DPE=∠α. 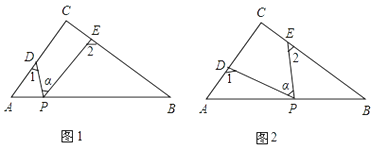
(1)若点P在线段AB上,如图(1),∠α=50°,则∠1+∠2=°
(2)若点P在边AB上运动,如图(2)所示,则∠α、∠1、∠2之间的关系为:
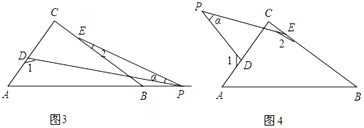
(3)若点P运动到边AB的延长线上,如图(3)所示,则∠α、∠1、∠2之间有何关系?猜想并说明理由.
(4)若点P运动到△ABC形外,如图(4),则∠α、∠1、∠2之间的关系为: .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com