
【题目】Rt△ABC中,∠C=90°,点D、E是△ABC边AC、BC上的点,点P是一动点.令∠PDA=∠1,∠PEB=∠2,∠DPE=∠α. 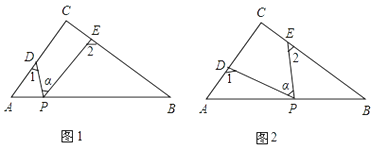
(1)若点P在线段AB上,如图(1),∠α=50°,则∠1+∠2=°
(2)若点P在边AB上运动,如图(2)所示,则∠α、∠1、∠2之间的关系为:
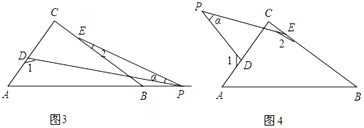
(3)若点P运动到边AB的延长线上,如图(3)所示,则∠α、∠1、∠2之间有何关系?猜想并说明理由.
(4)若点P运动到△ABC形外,如图(4),则∠α、∠1、∠2之间的关系为: .
【答案】
(1)140
(2)∠1+∠2=90°+α
(3)解:∠1=90°+∠2+α,
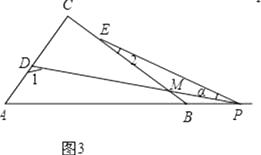
理由:如图3,∵∠2+∠α=∠DME,∠DME+∠C=∠1,
∴∠1=∠C+∠2+α=90°+∠2+α
(4)∠2=90°+∠1﹣α
【解析】解:(1.)∵∠1+∠2+∠CDP+∠CEP=360°,∠C+∠α+∠CDP+∠CEP=360°, ∴∠1+∠2=∠C+∠α,
∵∠C=90°,∠α=50°,
∴∠1+∠2=140°,
所以答案是:140;
(2.)∵∠1+∠2+∠CDP+∠CEP=360°,∠C+∠α+∠CDP+∠CEP=360°,
∴∠α+∠C=∠1+∠2,
∴∠1+∠2=90°+α,
所以答案是:∠1+∠2=90°+α;
(4.)如图4,∵∠PFD=∠EFC,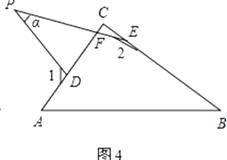
∴180°﹣∠PFD=180°﹣∠EFC,
∴∠α+180°﹣∠1=∠C+180°﹣∠2,
∴∠2=90°+∠1﹣α,
所以答案是:∠2=90°+∠1﹣α.
【考点精析】利用三角形的内角和外角和三角形的外角对题目进行判断即可得到答案,需要熟知三角形的三个内角中,只可能有一个内角是直角或钝角;直角三角形的两个锐角互余;三角形的一个外角等于和它不相邻的两个内角的和;三角形的一个外角大于任何一个和它不相邻的内角;三角形一边与另一边的延长线组成的角,叫三角形的外角;三角形的一个外角等于和它不相邻的两个内角的和;三角形的一个外角大于任何一个和它不相邻的内角.


科目:初中数学 来源: 题型:
【题目】梧州市特产批发市场有龟苓膏粉批发,其中A品牌的批发价是每包20元,B品牌的批发价是每包25元,小王需购买A、B两种品牌的龟苓膏共1000包.
(1)若小王按需购买A、B两种品牌龟苓膏粉共用22000元,则各购买多少包?
(2)凭会员卡在此批发市场购买商品可以获得8折优惠,会员卡费用为500元.若小王购买会员卡并用此卡按需购买1000包龟苓膏粉,共用了y元,设A品牌买了x包,请求出y与x之间的函数关系式.
(3)在(2)中,小王共用了20000元,他计划在网店包邮销售这批龟苓膏粉,每包龟苓膏粉小王需支付邮费8元,若每包销售价格A品牌比B品牌少5元,请你帮他计算,A品牌的龟苓膏粉每包定价不低于多少元时才不亏本(运算结果取整数)?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,点 ![]() 为直线
为直线 ![]() 上一点,过点
上一点,过点 ![]() 作射线
作射线 ![]() ,使
,使 ![]() ,将一直角三角板的直角顶点放在点
,将一直角三角板的直角顶点放在点 ![]() 处,一边
处,一边 ![]() 在射线
在射线 ![]() 上,另一边
上,另一边 ![]() 在直线
在直线 ![]() 的下方.
的下方.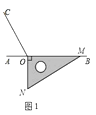
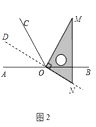
(1)将图1中的三角板绕点 ![]() 逆时针旋转至图
逆时针旋转至图 ![]() ,使一边
,使一边 ![]() 在
在 ![]() 的内部,且恰好平分
的内部,且恰好平分 ![]() ,问:此时直线
,问:此时直线 ![]() 是否平分
是否平分 ![]() ?请直接写出结论:直线
?请直接写出结论:直线 ![]() (平分或不平分)
(平分或不平分) ![]() .
.
(2)将图1中的三角板绕点 ![]() 以每秒
以每秒 ![]() 的速度沿逆时针方向旋转一周,在旋转的过程中,第
的速度沿逆时针方向旋转一周,在旋转的过程中,第 ![]() 秒时,直线
秒时,直线 ![]() 恰好平分锐角
恰好平分锐角 ![]() ,则
,则 ![]() 的值为.(直接写出结果)
的值为.(直接写出结果)
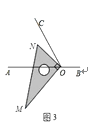
(3)将图1中的三角板绕点 ![]() 顺时针旋转,请探究:当
顺时针旋转,请探究:当 ![]() 始终在
始终在 ![]() 的内部时(如图3),
的内部时(如图3), ![]() 与
与 ![]() 的差是否发生变化?若不变,请求出这个差值;若变化,请举例说明.
的差是否发生变化?若不变,请求出这个差值;若变化,请举例说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在矩形纸片ABCD中,AB=3,AD=5.如图所示,折叠纸片,使点A落在BC边上的A′处,折痕为PQ,当点A′在BC边上移动时,折痕的端点P.Q也随之移动,若限定点P,Q分别在线段AB,AD边上移动,则点A′在BC边上可移动的最大距离为( ) 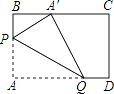
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】盘锦红海滩景区门票价格80元/人,景区为吸引游客,对门票价格进行动态管理,非节假日打a折,节假日期间,10人以下(包括10人)不打折,10人以上超过10人的部分打b折,设游客为x人,门票费用为y元,非节假日门票费用y1(元)及节假日门票费用y2(元)与游客x(人)之间的函数关系如图所示. 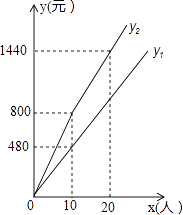
(1)a= , b=;
(2)直接写出y1、y2与x之间的函数关系式;
(3)导游小王6月10日(非节假日)带A旅游团,6月20日(端午节)带B旅游团到红海滩景区旅游,两团共计50人,两次共付门票费用3040元,求A、B两个旅游团各多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
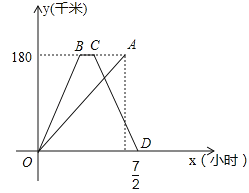
【题目】快、慢两车分别从相距180千米的甲、乙两地同时出发,沿同一路线匀速行驶,相向而行,快车到达乙地停留一段时间后,按原路原速返回甲地.慢车到达甲地比快车到达甲地早![]() 小时,慢车速度是快车速度的一半,快、慢两车到达甲地后停止行驶,两车距各自出发地的路程y(千米)与所用时间x(小时)的函数图象如图所示,请结合图象信息解答下列问题:
小时,慢车速度是快车速度的一半,快、慢两车到达甲地后停止行驶,两车距各自出发地的路程y(千米)与所用时间x(小时)的函数图象如图所示,请结合图象信息解答下列问题:
(1)请直接写出快、慢两车的速度;
(2)求快车返回过程中y(千米)与x(小时)的函数关系式;
(3)两车出发后经过多长时间相距90千米的路程?直接写出答案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算下列各题:
(1)![]() +(-
+(- ![]() )-(-
)-(- ![]() )+(+
)+(+ ![]() );
);
(2)![]() +(-71) +
+(-71) + ![]() +(-9 );
+(-9 );
(3)-9 ![]() ×81
×81
(4)(﹣36)×(﹣ ![]() +
+ ![]() ﹣
﹣ ![]() )
)
(5)-15+(-2)2×( ![]() -
- ![]() )-
)- ![]() ÷3;
÷3;
(6)![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道,可以单独用正三角形、正方形或正六边形镶嵌平面.
如果我们要同时用两种不同的正多边形镶嵌平面,可能设计出几种不同的组合方案?
问题解决:
猜想1:是否可以同时用正方形、正八边形两种正多边形组合进行平面镶嵌?
验证1:在镶嵌平面时,设围绕某一点有x个正方形和y个正八边形的内角可以拼成一个周角.根据题意,可得方程:90x+ ![]() y=360,整理得:2x+3y=8,
y=360,整理得:2x+3y=8,
我们可以找到方程的正整数解为 ![]() .
.
结论1:镶嵌平面时,在一个顶点周围围绕着1个正方形和2个正八边形的内角可以拼成一个周角,所以同时用正方形和正八边形两种正多边形组合可以进行平面镶嵌.
猜想2:是否可以同时用正三角形和正六边形两种正多边形组合进行平面镶嵌?若能,请按照上述方法进行验证,并写出所有可能的方案;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,O为坐标原点,四边形OACB是菱形,OB在x轴的正半轴上,sin∠AOB=![]() ,反比例函数
,反比例函数![]() 在第一象限内的图象经过点A,与BC交于点F,则△AOF的面积等于( )
在第一象限内的图象经过点A,与BC交于点F,则△AOF的面积等于( )
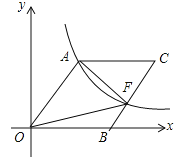
A.60 B.80 C.30 D.40
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com