
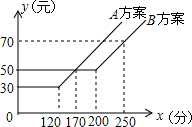
 ��ͼ��ij���Ź�˾�ṩ��A��B���ַ������ƶ�ͨѶ����y��Ԫ����ͨ��ʱ��x���֣�֮��Ĺ�ϵ�������н�������ȷ�Ĺ��У�������
��ͼ��ij���Ź�˾�ṩ��A��B���ַ������ƶ�ͨѶ����y��Ԫ����ͨ��ʱ��x���֣�֮��Ĺ�ϵ�������н�������ȷ�Ĺ��У�������| A�� | 1�� | B�� | 2�� | C�� | 3�� | D�� | 4�� |
���� ����ͼ��֪������ͨ��170�����շ�һ������ͨ��120ʱA�շ�30Ԫ��B�շ�50Ԫ������A����120���Ӻ�ÿ���Ӽ���0.4Ԫ��B����200���Ӽ���ÿ����0.4Ԫ���ɴ˼���ȷ���м�����ȷ��
��� �⣺�������
A����1����0��x��120��yA=30��
��2����x��120��yA=30+��x-120����[��50-30���£�170-120��]=0.4x-18��
B����1����0��x��200��yB=50��
��x��200��yB=50+[��70-50���£�250-200��]��x-200��=0.4x-30��
���Ե�x��120ʱ��A������B��������20Ԫ���ʣ�1����ȷ��
��x��200ʱ��B������A��������12Ԫ���ʣ�2����ȷ��
��y=60ʱ��A��60=0.4x-18����x=195��
B��60=0.4x-30����x=225���ʣ�3����ȷ��
��A������B�����ķ�����ȣ�ͨ��ʱ��Ϊ170���ӣ��ʣ�4����ȷ��
��ѡ��D��
���� ������Ҫ�����˺���ͼ������ʣ�����Ĺؼ��Ǵ�ͼ�����ҳ���������Ϣ������⣮


 �ƸԴ��ž�ϵ�д�
�ƸԴ��ž�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| x | -4.1 | -4.2 | -4.3 | -4.4 |
| x2+2x-k | -1.39 | -0.76 | -0.11 | 0.56 |
| A�� | -4.1 | B�� | -4.2 | C�� | -4.3 | D�� | -4.4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����ƽ��ֱ������ϵ�У���ABC�������������ֱ�ΪA��-1��3����B��-3��2����C��0��1����������ABC������������ԭ��O�ԳƵġ�A1B1C1��
��ͼ����ƽ��ֱ������ϵ�У���ABC�������������ֱ�ΪA��-1��3����B��-3��2����C��0��1����������ABC������������ԭ��O�ԳƵġ�A1B1C1���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
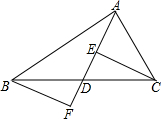 ��ͼ���ڡ�ABC�У���DΪBC���ϵ��е㣬����AD����EΪ�߶�AD�ϵ�һ�㣬����CE������B��BF��CE��AD���ӳ����ڵ�F����֤��CE=BF��
��ͼ���ڡ�ABC�У���DΪBC���ϵ��е㣬����AD����EΪ�߶�AD�ϵ�һ�㣬����CE������B��BF��CE��AD���ӳ����ڵ�F����֤��CE=BF���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
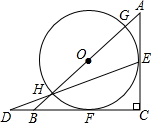 ��ͼ���ڵ���ֱ�������Ρ�ABC�У���ACB=90�㣬��б��AB�ϵĵ�OΪԲ�ĵ�Բ�ֱ���AC��BC������E��F����AB�ֱ��ڵ�G��H����EH���ӳ��ߺ�CB���ӳ��߽��ڵ�D��
��ͼ���ڵ���ֱ�������Ρ�ABC�У���ACB=90�㣬��б��AB�ϵĵ�OΪԲ�ĵ�Բ�ֱ���AC��BC������E��F����AB�ֱ��ڵ�G��H����EH���ӳ��ߺ�CB���ӳ��߽��ڵ�D���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
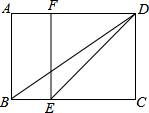 ��֪����ͼ���ھ���ABCD�У�E��BC����һ�㣬DEƽ�֡�ADC��EF��DC��AD���ڵ�F������BD��
��֪����ͼ���ھ���ABCD�У�E��BC����һ�㣬DEƽ�֡�ADC��EF��DC��AD���ڵ�F������BD���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ������A1B1C1O��A2B2C2C1����ͼ��ʾ��ʽ���ã���A1��A2��ֱ��y=x+1�ϣ���C1��C2��x���ϣ���֪A1��������ǣ�0��1�������B2������Ϊ��3��2����
������A1B1C1O��A2B2C2C1����ͼ��ʾ��ʽ���ã���A1��A2��ֱ��y=x+1�ϣ���C1��C2��x���ϣ���֪A1��������ǣ�0��1�������B2������Ϊ��3��2�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
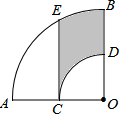 ��ͼ��������AOB�У���AOB=90�㣬��CΪOA���е㣬CE��OA��$\widehat{AB}$�ڵ�E���Ե�OΪԲ�ģ�OC�ij�Ϊ�뾶��$\widehat{CD}$��OB�ڵ�D����OA=2������Ӱ���ֵ����Ϊ$\frac{��}{12}$+$\frac{\sqrt{3}}{2}$��
��ͼ��������AOB�У���AOB=90�㣬��CΪOA���е㣬CE��OA��$\widehat{AB}$�ڵ�E���Ե�OΪԲ�ģ�OC�ij�Ϊ�뾶��$\widehat{CD}$��OB�ڵ�D����OA=2������Ӱ���ֵ����Ϊ$\frac{��}{12}$+$\frac{\sqrt{3}}{2}$���鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com