
ЁОЬтФПЁПЃЈ1ЃЉЙлВьЭМаЮЃК
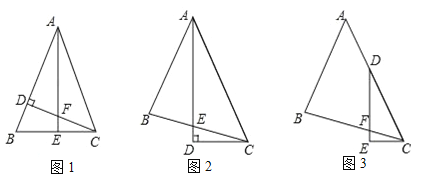
ШчЭМ1ЃЌЁїABCжаЃЌAB=ACЃЌЁЯBAC=45ЁуЃЌCDЁЭABЃЌAEЁЭBCЃЌДЙзуЗжБ№ЮЊDЁЂEЃЌCDгыAEНЛгкЕуFЃЎ
ЂйаДГіЭМ1жаЫљгаЕФШЋЕШШ§НЧаЮ_________________ЃЛ
ЂкЯпЖЮAFгыЯпЖЮCEЕФЪ§СПЙиЯЕЪЧ_________________ЃЛ
ЃЈ2ЃЉЮЪЬтЬНОПЃК
ШчЭМ2ЃЌЁїABCжаЃЌЁЯBAC=45ЁуЃЌAB=BCЃЌADЦНЗжЁЯBACЃЌADЁЭCDЃЌДЙзуЮЊDЃЌADгыBCНЛгкЕуEЃЎ
ЧѓжЄЃКAE=2CDЃЎ
ЃЈ3ЃЉЭиеЙбгЩьЃК
ШчЭМ3ЃЌЁїABCжаЃЌЁЯBAC=45ЁуЃЌAB=BCЃЌЕуDдкACЩЯЃЌЁЯEDC=![]() ЁЯBACЃЌDEЁЭCEЃЌДЙзуЮЊEЃЌDEгыBCНЛгкЕуFЃЎ
ЁЯBACЃЌDEЁЭCEЃЌДЙзуЮЊEЃЌDEгыBCНЛгкЕуFЃЎ
ЧѓжЄЃКDF=2CEЃЎ
ЁОД№АИЁПЃЈ1ЃЉЂйЁїABEЁеЁїACEЃЌЁїADFЁеЁїCDBЃЛЂкAF=2CEЃЛЃЈ2ЃЉД№АИМћНтЮіЃЛЃЈ3ЃЉД№АИМћНтЮі
ЁОНтЮіЁП
ЪдЬт![]() ЙлВьЭМаЮЃКЂйгЩШЋЕШШ§НЧаЮЕФХаЖЈЗНЗЈШнвзЕУГіНсЙћЃЛ
ЙлВьЭМаЮЃКЂйгЩШЋЕШШ§НЧаЮЕФХаЖЈЗНЗЈШнвзЕУГіНсЙћЃЛ
ЂкгЩШЋЕШШ§НЧаЮЕФаджЪМДПЩЕУГіНсТлЃЛ![]() ЮЪЬтЬНОПЃКбгГЄ
ЮЪЬтЬНОПЃКбгГЄ![]() НЛгкЕу
НЛгкЕу![]() ЃЌгЩASAжЄУї
ЃЌгЩASAжЄУї![]() Ёе
Ёе![]() ЃЌЕУГіЖдгІБпЯрЕШ
ЃЌЕУГіЖдгІБпЯрЕШ![]() МД
МД![]() жЄГі
жЄГі![]() гЩASAжЄУї
гЩASAжЄУї![]() Ёе
Ёе![]() ЕУГі
ЕУГі![]() МДПЩЃЎ
МДПЩЃЎ![]() ЭиеЙбгЩьЃКзїDGЁЭBCгкЕуHЃЌНЛCEЕФбгГЄЯпгкGЃЌЭЌЩЯжЄУїШ§НЧаЮШЋЕШЃЌЕУГі
ЭиеЙбгЩьЃКзїDGЁЭBCгкЕуHЃЌНЛCEЕФбгГЄЯпгкGЃЌЭЌЩЯжЄУїШ§НЧаЮШЋЕШЃЌЕУГі![]() МДПЩЃЎ
МДПЩЃЎ
ЪдЬтНтЮіЃК
ЃЈ1ЃЉЙлВьЭМаЮЃК
ЂйЁїABEЁеЁїACEЃЌЁїADFЁеЁїCDBЃЛ
ЂкAF=2CEЃЛ
ЃЈ2ЃЉЮЪЬтЬНОПЃК
жЄУїЃКбгГЄABЁЂCDНЛгкЕуGЃЌШчЭМ2ЫљЪОЃК
ЁпADЦНЗжЁЯBACЃЌ
ЁрЁЯCAD=ЁЯGADЃЌ
ЁпADЁЭCDЃЌ
ЁрЁЯADC=ЁЯADG=90ЁуЃЌ
дкЁїADCКЭЁїADGжаЃЌ
 ЃЌ
ЃЌ
ЁрЁїADCЁеЁїADGЃЈASAЃЉЃЌ
ЁрCD=GDЃЌ
МДCG=2CDЃЌ
ЁпЁЯBAC=45ЁуЃЌAB=BCЃЌ
ЁрЁЯABC=90ЁуЃЌ
ЁрЁЯCBG=90ЁуЃЌ
ЁрЁЯG+ЁЯBCG=90ЁуЃЌ
ЁпЁЯG+ЁЯBAE=90ЁуЃЌ
ЁрЁЯBAE=ЁЯBCGЃЌ
дкЁїABEКЭЁїCBGжаЃЌ
ЁрЁїADCЁеЁїCBGЃЈASAЃЉЃЌ
ЁрAE=CG=2CDЃЎ
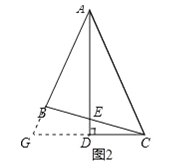
ЃЈ3ЃЉЭиеЙбгЩьЃК
жЄУїЃКзїDGЁЭBCгкЕуHЃЌНЛCEЕФбгГЄЯпгкGЃЌ
ЁпЁЯBAC=45ЁуЃЌAB=BCЃЌ
ЁрABЁЭBCЃЌ
ЁрDGЁЮABЃЌ
ЁрЁЯGDC=ЁЯBAC=45ЁуЃЌ
ЁрЁЯEDC=![]() ЁЯBAC=22.5Ёу=ЁЯEDGЃЌDH=CHЃЌ
ЁЯBAC=22.5Ёу=ЁЯEDGЃЌDH=CHЃЌ
гжЁпDEЁЭCEЃЌ
ЁрЁЯDEC=ЁЯDEG=90ЁуЃЌ
дкЁїDECКЭЁїDEGжаЃЌ
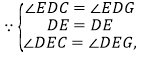
ЁрЁїDECЁеЁїDEGЃЈASAЃЉЃЌ
ЁрDC=DGЃЌCG=2CEЃЌ
ЁпЁЯDHF=ЁЯCEF=90ЁуЃЌЁЯDFH=ЁЯCFEЃЌ
ЁрЁЯFDH=ЁЯGCHЃЌ
дкЁїDHFКЭЁїCHGжаЃЌ
ЁрЁїDHFЁеЁїCHGЃЈASAЃЉ,
ЁрDF=CG=2CEЃЎ


 жаПМНтЖСПМЕуОЋСЗЯЕСаД№АИ
жаПМНтЖСПМЕуОЋСЗЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЁїABCКЭЁїDBEжаЃЌBC=BEЃЌЛЙашдйЬэМгСНИіЬѕМўВХФмЪЙЁїABCЁеЁїDBEЃЌдђВЛФмЬэМгЕФвЛзщЬѕМўЪЧЃЈ ЃЉ

A. AB=DBЃЌЁЯ A=ЁЯ D B. DB=ABЃЌAC=DE C. AC=DEЃЌЁЯC=ЁЯE D. ЁЯ C=ЁЯ EЃЌЁЯ A=ЁЯ D
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЁїABCжаЃЌЁЯB=60ЁуЃЌЁЯC=75ЁуЃЌAC=3 ![]() ЃЌЧѓABЕФГЄЃЎ
ЃЌЧѓABЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
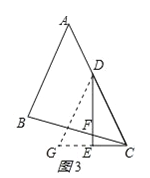
ЁОЬтФПЁПШчЭМЃЌCЃЌEЪЧжБЯпlСНВрЕФЕуЃЌвдCЮЊдВаФЃЌCEГЄЮЊАыОЖЛЛЁНЛlгкAЃЌBСНЕуЃЌгжЗжБ№вдAЃЌBЮЊдВаФЃЌДѓгк ![]() ABЕФГЄЮЊАыОЖЛЛЁЃЌСНЛЁНЛгкЕуDЃЌСЌНгCAЃЌCBЃЌCDЃЌЯТСаНсТлВЛвЛЖЈе§ШЗЕФЪЧЃЈ ЃЉ
ABЕФГЄЮЊАыОЖЛЛЁЃЌСНЛЁНЛгкЕуDЃЌСЌНгCAЃЌCBЃЌCDЃЌЯТСаНсТлВЛвЛЖЈе§ШЗЕФЪЧЃЈ ЃЉ 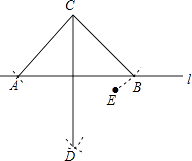
A.CDЁЭl
B.ЕуAЃЌBЙигкжБЯпCDЖдГЦ
C.ЕуCЃЌDЙигкжБЯпlЖдГЦ
D.CDЦНЗжЁЯACB
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЯШЛЏМђЃК ![]() ЁТ
ЁТ ![]() +
+ ![]() ЃЌдйЧѓЕБx+1гыx+6ЛЅЮЊЯрЗДЪ§ЪБДњЪ§ЪНЕФжЕЃЎ
ЃЌдйЧѓЕБx+1гыx+6ЛЅЮЊЯрЗДЪ§ЪБДњЪ§ЪНЕФжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌХзЮяЯпy=ax2+2ax+cНЛxжсгкAЃЌBСНЕуЃЌНЛyжсгкЕуCЃЈ0ЃЌ3ЃЉЃЌtanЁЯOAC= ![]() ЃЎ
ЃЎ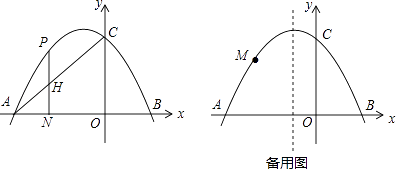
ЃЈ1ЃЉЧѓХзЮяЯпЕФНтЮіЪНЃЛ
ЃЈ2ЃЉЕуHЪЧЯпЖЮACЩЯШЮвтвЛЕуЃЌЙ§HзїжБЯпHNЁЭxжсгкЕуNЃЌНЛХзЮяЯпгкЕуPЃЌЧѓЯпЖЮPHЕФзюДѓжЕЃЛ
ЃЈ3ЃЉЕуMЪЧХзЮяЯпЩЯШЮвтвЛЕуЃЌСЌНгCMЃЌвдCMЮЊБпзїе§ЗНаЮCMEFЃЌЪЧЗёДцдкЕуMЪЙЕуEЧЁКУТфдкЖдГЦжсЩЯЃПШєДцдкЃЌЧыЧѓГіЕуMЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПНтД№
ЃЈ1ЃЉвбжЊЉ ![]() гыxnym+nЪЧЭЌРрЯюЃЌЧѓmЁЂnЕФжЕЃЛ
гыxnym+nЪЧЭЌРрЯюЃЌЧѓmЁЂnЕФжЕЃЛ
ЃЈ2ЃЉЯШЛЏМђКѓЧѓжЕЃКЃЈ ![]() ЃЉ
ЃЉ ![]() ЃЌЦфжаa=
ЃЌЦфжаa= ![]() ЃЎ
ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкОиаЮABCDжаЃЈADЃОABЃЉЃЌЕуEЪЧBCЩЯвЛЕуЃЌЧвDE=DAЃЌAFЁЭDEЃЌДЙзуЮЊЕуFЃЌдкЯТСаНсТлжаЃЌВЛвЛЖЈе§ШЗЕФЪЧЃЈЁЁЁЁЃЉ
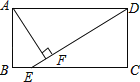
A. ЁїAFDЁеЁїDCE B. AF=![]() AD C. AB=AF D. BE=ADЉDF
AD C. AB=AF D. BE=ADЉDF
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМ1ЃЈзЂЃКгыЭМ2ЭъШЋЯрЭЌЃЉЃЌЖўДЮКЏЪ§y= ![]() x2+bx+cЕФЭМЯѓгыxжсНЛгкAЃЈ3ЃЌ0ЃЉЃЌBЃЈЉ1ЃЌ0ЃЉСНЕуЃЌгыyжсНЛгкЕуCЃЎ
x2+bx+cЕФЭМЯѓгыxжсНЛгкAЃЈ3ЃЌ0ЃЉЃЌBЃЈЉ1ЃЌ0ЃЉСНЕуЃЌгыyжсНЛгкЕуCЃЎ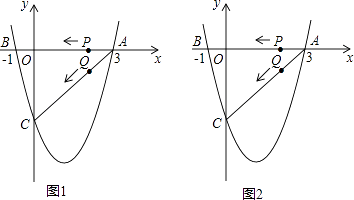
ЃЈ1ЃЉЧѓИУЖўДЮКЏЪ§ЕФНтЮіЪНЃЛ
ЃЈ2ЃЉЩшИУХзЮяЯпЕФЖЅЕуЮЊDЃЌЧѓЁїACDЕФУцЛ§ЃЈЧыдкЭМ1жаЬНЫїЃЉЃЛ
ЃЈ3ЃЉШєЕуPЃЌQЭЌЪБДгAЕуГіЗЂЃЌЖМвдУПУы1ИіЕЅЮЛГЄЖШЕФЫйЖШЗжБ№биABЃЌACБпдЫЖЏЃЌЦфжавЛЕуЕНДяЖЫЕуЪБЃЌСэвЛЕувВЫцжЎЭЃжЙдЫЖЏЃЌЕБPЃЌQдЫЖЏЕНtУыЪБЃЌЁїAPQбиPQЫљдкЕФжБЯпЗелЃЌЕуAЧЁКУТфдкХзЮяЯпЩЯEЕуДІЃЌЧыжБНгХаЖЈДЫЪБЫФБпаЮAPEQЕФаЮзДЃЌВЂЧѓГіEЕузјБъЃЈЧыдкЭМ2жаЬНЫїЃЉЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com