
【题目】如图,在平面直角坐标系中,抛物线y=ax2+2ax+c交x轴于A,B两点,交y轴于点C(0,3),tan∠OAC= ![]() .
.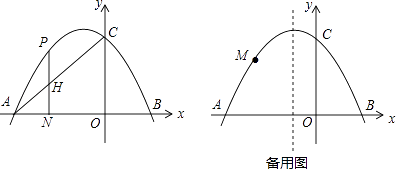
(1)求抛物线的解析式;
(2)点H是线段AC上任意一点,过H作直线HN⊥x轴于点N,交抛物线于点P,求线段PH的最大值;
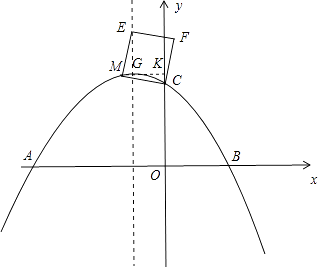
(3)点M是抛物线上任意一点,连接CM,以CM为边作正方形CMEF,是否存在点M使点E恰好落在对称轴上?若存在,请求出点M的坐标;若不存在,请说明理由.
【答案】
(1)
解:∵C(0,3),
∴OC=3,
∵tan∠OAC= ![]() ,
,
∴OA=4,
∴A(﹣4,0).
把A(﹣4,0)、C(0,3)代入y=ax2+2ax+c中,
得 ![]() ,解得:
,解得: 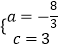 ,
,
∴抛物线的解析式为y=﹣ ![]() x2﹣
x2﹣ ![]() x+3
x+3
(2)
解:设直线AC的解析式为y=kx+b,
把A(﹣4,0)、C(0,3)代入y=kx+b中,
得: ![]() ,解得:
,解得: ![]() ,
,
∴直线AC的解析式为y= ![]() x+3.
x+3.
设N(x,0)(﹣4<x<0),则H(x, ![]() x+3),P(x,﹣
x+3),P(x,﹣ ![]() x2﹣
x2﹣ ![]() x+3),
x+3),
∴PH=﹣ ![]() x2﹣
x2﹣ ![]() x+3﹣(
x+3﹣( ![]() x+3)=﹣
x+3)=﹣ ![]() x2﹣
x2﹣ ![]() x=﹣
x=﹣ ![]() (x+2)2+
(x+2)2+ ![]() ,
,
∵﹣ ![]() <0,
<0,
∴PH有最大值,
当x=﹣2时,PH取最大值,最大值为 ![]()
(3)
解:过点M作MK⊥y轴于点K,交对称轴于点G,则∠MGE=∠MKC=90°,
∴∠MEG+∠EMG=90°,
∵四边形CMEF是正方形,
∴EM=MC,∠MEC=90°,
∴∠EMG+∠CMK=90°,
∴∠MEG=∠CMK.
在△MCK和△MEG中, 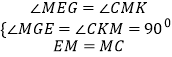 ,
,
∴△MCK≌△MEG(AAS),
∴MG=CK.
由抛物线的对称轴为x=﹣1,设M(x,﹣ ![]() x2﹣
x2﹣ ![]() x+3),则G(﹣1,﹣
x+3),则G(﹣1,﹣ ![]() x2﹣
x2﹣ ![]() x+3),K(0,﹣
x+3),K(0,﹣ ![]() x2﹣
x2﹣ ![]() x+3),
x+3),
∴MG=|x+1|,CK=|﹣ ![]() x2﹣
x2﹣ ![]() x+3﹣3|=|﹣
x+3﹣3|=|﹣ ![]() x2﹣
x2﹣ ![]() x|=|
x|=| ![]() x2+
x2+ ![]() x|,
x|,
∴|x+1|=| ![]() x2+
x2+ ![]() x|,
x|,
∴ ![]() x2+
x2+ ![]() x=±(x+1),
x=±(x+1),
解得:x1=﹣4,x2=﹣ ![]() ,x3=﹣
,x3=﹣ ![]() ,x4=2,
,x4=2,
代入抛物线解析式得:y1=0,y2= ![]() ,y3=
,y3= ![]() ,y4=0,
,y4=0,
∴点M的坐标是(﹣4,0),(﹣ ![]() ,
, ![]() ),(﹣
),(﹣ ![]() ,
, ![]() )或(2,0).
)或(2,0).
【解析】(1)由点C的坐标以及tan∠OAC= ![]() 可得出点A的坐标,结合点A、C的坐标利用待定系数法即可求出抛物线的解析式;(2)设直线AC的解析式为y=kx+b,由点A、C的解析式利用待定系数法即可求出直线AC的解析式,设N(x,0)(﹣4<x<0),可找出H、P的坐标,由此即可得出PH关于x的解析式,利用配方法即二次函数的性质即可解决最值问题;(3)过点M作MK⊥y轴于点K,交对称轴于点G,根据角的计算依据正方形的性质即可得出△MCK≌△MEG(AAS),进而得出MG=CK.设出点M的坐标利用正方形的性质即可得出点G、K的坐标,由正方形的性质即可得出关于x的含绝对值符号的一元二次方程,解方程即可求出x值,将其代入抛物线解析式中即可求出点M的坐标.本题考查了待定系数法求函数解析式、二次函数的性质、正方形的性质以及全等三角形的判定与性质,解题的关键是:(1)利用待定系数法求出抛物线解析式;(2)根据二次函数的性质解决最值问题;(3)根据正方形的性质得出关于x的含绝对值符号的一元二次方程.本题属于中档题,难度不大,解决该题型题目时,根据正方形的性质找出关于x的含绝对值符号的一元二次方程,解方程求出点的横坐标是关键.
可得出点A的坐标,结合点A、C的坐标利用待定系数法即可求出抛物线的解析式;(2)设直线AC的解析式为y=kx+b,由点A、C的解析式利用待定系数法即可求出直线AC的解析式,设N(x,0)(﹣4<x<0),可找出H、P的坐标,由此即可得出PH关于x的解析式,利用配方法即二次函数的性质即可解决最值问题;(3)过点M作MK⊥y轴于点K,交对称轴于点G,根据角的计算依据正方形的性质即可得出△MCK≌△MEG(AAS),进而得出MG=CK.设出点M的坐标利用正方形的性质即可得出点G、K的坐标,由正方形的性质即可得出关于x的含绝对值符号的一元二次方程,解方程即可求出x值,将其代入抛物线解析式中即可求出点M的坐标.本题考查了待定系数法求函数解析式、二次函数的性质、正方形的性质以及全等三角形的判定与性质,解题的关键是:(1)利用待定系数法求出抛物线解析式;(2)根据二次函数的性质解决最值问题;(3)根据正方形的性质得出关于x的含绝对值符号的一元二次方程.本题属于中档题,难度不大,解决该题型题目时,根据正方形的性质找出关于x的含绝对值符号的一元二次方程,解方程求出点的横坐标是关键.
【考点精析】通过灵活运用二次函数的性质和正方形的性质,掌握增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小;正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形即可以解答此题.


科目:初中数学 来源: 题型:
【题目】如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),
C(3,4)
⑴ 作出与△ABC关于y轴对称△A1B1C1,并写出 三个顶点的坐标为:A1( ),B1( ),C1( );
⑵ 在x轴上找一点P,使PA+PB的值最小,请直接写出点P的坐标;
⑶ 在 y 轴上是否存在点 Q,使得S△AOQ=![]() S△ABC,如果存在,求出点 Q 的坐标,如果不存在,说明理由。
S△ABC,如果存在,求出点 Q 的坐标,如果不存在,说明理由。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某县为了落实中央的“强基惠民工程”,计划将某村的居民自来水管道进行改造.该工程若由甲队单独施工恰好在规定时间内完成;若乙队单独施工,则完成工程所需天数是规定天数的1.5倍.如果由甲、乙队先合做15天,那么余下的工程由甲队单独完成还需5天.
(1)这项工程的规定时间是多少天?
(2)已知甲队每天的施工费用为6500元,乙队每天的施工费用为3500元.为了缩短工期以减少对居民用水的影响,工程指挥部最终决定该工程由甲、乙队合做来完成.则该工程施工费用是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程解应用题
北京时间2015年7月31日,国际奥委会主席巴赫宣布:中国北京获得2022年第24界冬季奥林匹克运动会举办权,近期,新建北京至张家口铁路可行性研究报告已经获得国家发改委批复,铁路全长约180千米,按照设计,京张高铁列车的平均行驶速度是普通快车的1.5倍,用时比普通快车用时少了20分钟,求京张高铁列车的平均行驶速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
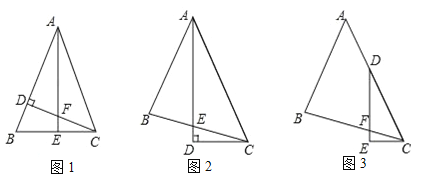
【题目】(1)观察图形:
如图1,△ABC中,AB=AC,∠BAC=45°,CD⊥AB,AE⊥BC,垂足分别为D、E,CD与AE交于点F.
①写出图1中所有的全等三角形_________________;
②线段AF与线段CE的数量关系是_________________;
(2)问题探究:
如图2,△ABC中,∠BAC=45°,AB=BC,AD平分∠BAC,AD⊥CD,垂足为D,AD与BC交于点E.
求证:AE=2CD.
(3)拓展延伸:
如图3,△ABC中,∠BAC=45°,AB=BC,点D在AC上,∠EDC=![]() ∠BAC,DE⊥CE,垂足为E,DE与BC交于点F.
∠BAC,DE⊥CE,垂足为E,DE与BC交于点F.
求证:DF=2CE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程组解应用题:打折前,买 10 件 A 商品和 5 件 B 商品共用了 400 元,买 5 件 A 商品和 10件 B 商品共用了 350 元.
(1)求打折前 A 商品、B 商品每件分别多少钱?
(2)打折后,买 100 件 A 商品和 100 件 B 商品共用了 3800 元.比不打折少花多少钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在日常生活中,如取款、上网等都需要密码.有一种用“因式分解”法产生的密码,方便记忆.原理是:如对于多项式x4-y4,因式分解的结果是(x-y)(x+y)·(x2+y2),若取x=9,y=9时,则各个因式的值是:(x-y)=0,(x+y)=18,x2+y2=162,于是就可以把“018162”作为一个六位数的密码.对于多项式4x3-xy2,取x=10,y=10时,用上述方法产生的密码共有多少种?请你分别写出来.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在菱形ABCD中,F为边BC的中点,DF与对角线AC交于点M,过M作ME⊥CD于点E,∠1=∠2.
(1)若CE=1,求BC的长;
(2)求证:AM=DF+ME.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com