
【题目】列方程组解应用题:打折前,买 10 件 A 商品和 5 件 B 商品共用了 400 元,买 5 件 A 商品和 10件 B 商品共用了 350 元.
(1)求打折前 A 商品、B 商品每件分别多少钱?
(2)打折后,买 100 件 A 商品和 100 件 B 商品共用了 3800 元.比不打折少花多少钱?
【答案】(1)A商品30元,B商品20元;(2)少1200元
【解析】
试题(1)本题的等量关系可表示为:打折前:10件A商品的钱数+5件B商品的钱数=400元;5件A商品的钱数+10件B商品的钱数=350元.据此列出方程组求出打折前A商品、B商品每件分别多少钱;
(2)先由(1)得出的打折前A商品、B商品每件分别多少钱计算出买100件A商品和100件B商品共用多少钱与打折后,买100件A商品和100件B商品共用了3800元进行比较.
试题解析:解:(1)设打折前A商品每件x元、B商品每件y元,根据题意,得:
![]() ,解得:
,解得:![]() .
.
答:打折前A商品每件30元、B商品每件20元.
(2)打折前,买100件A商品和100件B商品共用:
100×30+100×20=5000 (元)
比不打折少花:5000﹣3800=1200 (元)
答:打折后,买100件A商品和100件B商品比不打折少花1200元.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,AB∥DE,AC∥DF,AC=DF,要使△ABC≌△DEF需再补充一个条件,下列条件中,不能选择的是( )
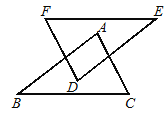
A. AB=DE B. BC=EF C. EF∥BC D. ∠B=∠E
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了倡导“节约用水,从我做起”的活动,某市政府决定对市直机关500户家庭的用水情况作一次调查,调查小组随机抽查了其中100户家庭一年的月平均用水量(单位:吨).并将调查结果制成了如图所示的条形统计图.
(1)求这100个样本数据的平均数、众数和中位数;
(2)根据样本数据,估计该市直机关500户家庭中月平均用水量不超过12吨的约有多少户?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在我们认识的多边形中,有很多轴对称图形.有些多边形,边数不同对称轴的条数也不同;有些多边形,边数相同但却有不同数目的对称轴.回答下列问题:
(1)非等边的等腰三角形有________条对称轴,非正方形的长方形有________条对称轴,等边三角形有___________条对称轴;
(2)观察下列一组凸多边形(实线画出),它们的共同点是只有1条对称轴,其中图1-2和图1-3都可以看作由图1-1修改得到的,仿照类似的修改方式,请你在图1-4和图1-5中,分别修改图1-2和图1-3,得到一个只有1条对称轴的凸五边形,并用实线画出所得的凸五边形;
(3)小明希望构造出一个恰好有2条对称轴的凸六边形,于是他选择修改长方形,图2中是他没有完成的图形,请用实线帮他补完整个图形;


(4)请你画一个恰好有3条对称轴的凸六边形,并用虚线标出对称轴.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线y=ax2+2ax+c交x轴于A,B两点,交y轴于点C(0,3),tan∠OAC= ![]() .
.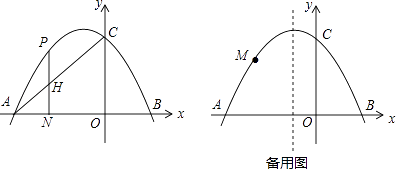
(1)求抛物线的解析式;
(2)点H是线段AC上任意一点,过H作直线HN⊥x轴于点N,交抛物线于点P,求线段PH的最大值;
(3)点M是抛物线上任意一点,连接CM,以CM为边作正方形CMEF,是否存在点M使点E恰好落在对称轴上?若存在,请求出点M的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠1=∠2,要得到△ABD≌△ACE,从下列条件中补选一个,则错误的是( )

A.AB=AC B.DB=EC C.∠ADB=∠AEC D.∠B=∠C
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校数学兴趣小组的成员小华对本班上学期期末考试数学成绩(成绩取整数,满分为100分)作了统计分析,绘制成如下频数分布表和频数分布直方图.

请你根据图表提供的信息,解答下列问题:
(1)频数分布表中a= ,b= ;
(2)补全频数分布直方图;
(3)数学老师准备从不低于90分的学生中选1人介绍学习经验,那么取得了93分的小华被选上的概率是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,AB=12,AD=8,∠ABC的平分线交CD于点F,交AD的延长线于点E,CG⊥BE,垂足为G,若EF=2,则线段CG的长为( ) 
A.![]()
B.4 ![]()
C.2 ![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,分别以Rt△ABC的直角边AC及斜边AB向外作等边△ACD及等边△ABE,已知:∠BAC=30°,EF⊥AB,垂足为F,连接DF. 
(1)试说明AC=EF;
(2)求证:四边形ADFE是平行四边形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com