
【题目】某校数学兴趣小组的成员小华对本班上学期期末考试数学成绩(成绩取整数,满分为100分)作了统计分析,绘制成如下频数分布表和频数分布直方图.

请你根据图表提供的信息,解答下列问题:
(1)频数分布表中a= ,b= ;
(2)补全频数分布直方图;
(3)数学老师准备从不低于90分的学生中选1人介绍学习经验,那么取得了93分的小华被选上的概率是 .
 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案科目:初中数学 来源: 题型:
【题目】已知:如图,线段AB和射线BM交于点B.
(1)利用尺规完成以下作图,并保留作图痕迹(不写作法)
①在射线BM上作一点C,使AC=AB;
②作∠ABM 的角平分线交AC于D点;
③在射线CM上作一点E,使CE=CD,连接DE.
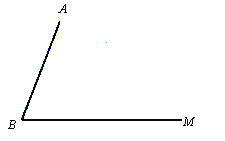
(2)在(1)所作的图形中,猜想线段BD与DE的数量关系,并证明之.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程解应用题
北京时间2015年7月31日,国际奥委会主席巴赫宣布:中国北京获得2022年第24界冬季奥林匹克运动会举办权,近期,新建北京至张家口铁路可行性研究报告已经获得国家发改委批复,铁路全长约180千米,按照设计,京张高铁列车的平均行驶速度是普通快车的1.5倍,用时比普通快车用时少了20分钟,求京张高铁列车的平均行驶速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程组解应用题:打折前,买 10 件 A 商品和 5 件 B 商品共用了 400 元,买 5 件 A 商品和 10件 B 商品共用了 350 元.
(1)求打折前 A 商品、B 商品每件分别多少钱?
(2)打折后,买 100 件 A 商品和 100 件 B 商品共用了 3800 元.比不打折少花多少钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在日常生活中,如取款、上网等都需要密码.有一种用“因式分解”法产生的密码,方便记忆.原理是:如对于多项式x4-y4,因式分解的结果是(x-y)(x+y)·(x2+y2),若取x=9,y=9时,则各个因式的值是:(x-y)=0,(x+y)=18,x2+y2=162,于是就可以把“018162”作为一个六位数的密码.对于多项式4x3-xy2,取x=10,y=10时,用上述方法产生的密码共有多少种?请你分别写出来.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标中,点A的坐标为(1,1),OA=AC,∠OAC=90°,点D为x轴上一动点.以AD为边在AD的右侧作正方形ADEF.
(1)当点D在线段OC上时(不与点O、C重合),则线段CF与OD之间的数量关系为 ;位置关系为 ,
(2)当点D在线段OC的延长线上时,(1)中的结论是否成立?若成立,请说明理由;若不成立,请举一反例;
(3)设D点坐标为(t,0),当D点从O点运动到C点时,用含t的代数式表示E点坐标,并直接写出E点所经过的路径长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在菱形ABCD中,F为边BC的中点,DF与对角线AC交于点M,过M作ME⊥CD于点E,∠1=∠2.
(1)若CE=1,求BC的长;
(2)求证:AM=DF+ME.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,OABC的边OC在x轴的正半轴上,OC=5,反比例函数y= ![]() (x>0)的图象经过点A(1,4).
(x>0)的图象经过点A(1,4).
(1)求反比例函数的关系式和点B的坐标;
(2)如图2,过BC的中点D作DP∥x轴交反比例函数图象于点P,连接AP、OP.
①求△AOP的面积;
②在OABC的边上是否存在点M,使得△POM是以PO为斜边的直角三角形?若存在,请求出所有符合条件的点M的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是正方形,点E,K分别在边BC,AB上,点G在BA的延长线上,且CE=BK=AG.
(1)求证:①DE=DG; ②DE⊥DG;
(2)尺规作图:以线段DE,DG为边作出正方形DEFG(要求:只保留作图痕迹,不写作法和证明);
(3)连接(2)中的KF,猜想并写出四边形CEFK是怎样的特殊四边形,并证明你的猜想;
(4)当![]() =
=![]() 时,请直接写出
时,请直接写出![]() 的值.
的值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com