
【题目】如图,四边形ABCD是正方形,点E,K分别在边BC,AB上,点G在BA的延长线上,且CE=BK=AG.
(1)求证:①DE=DG; ②DE⊥DG;
(2)尺规作图:以线段DE,DG为边作出正方形DEFG(要求:只保留作图痕迹,不写作法和证明);
(3)连接(2)中的KF,猜想并写出四边形CEFK是怎样的特殊四边形,并证明你的猜想;
(4)当![]() =
=![]() 时,请直接写出
时,请直接写出![]() 的值.
的值.

【答案】(1)见解析;(2)见解析;(3)见解析;(4)![]()
【解析】
试题(1)由已知证明DE、DG所在的三角形全等,再通过全等三角形的对应角相等等量代换得出∠EDG=90°即可;
(2)根据有一个角是直角的菱形是正方形,分别以点G、E为圆心以DG为半径画弧交点F,得到正方形DEFG;
(3)由已知首先根据一组对边平行且相等的四边形是平行四边形证出四边形CKGD是平行四边形,然后根据平行四边形的性质和正方形的性质即可证明四边形CEFK为平行四边形;
(4)设CE=x,则CB=nx,CD=nx,根据勾股定理表示出DE2,即可表示出正方形ABCD和正方形DEFG的面积,然后作比即可.
试题解析:(1)证明:∵四边形ABCD是正方形,
∴DC=DA,∠DCE=∠DAG=90°.
又∵CE=AG,
∴△DCE≌△DAG,
∴DE=DG,
∠EDC=∠GDA,
又∵∠ADE+∠EDC=90°,
∴∠ADE+∠GDA=90°,
∴DE⊥DG.
(2)解:如图.

(3)解:四边形CEFK为平行四边形.
证明:设CK、DE相交于M点
∵四边形ABCD和四边形DEFG都是正方形,
∴AB∥CD,AB=CD,EF=DG,EF∥DG,
∵BK=AG,
∴KG=AB=CD,
∴四边形CKGD是平行四边形,
∴CK=DG=EF,CK∥DG,
∴∠KME=∠GDE=∠DEF=90°,
∴∠KME+∠DEF=180°,
∴CK∥EF,
∴四边形CEFK为平行四边形.
(4)解:∵![]() ,
,
∴设CE=x,则CB=nx,
∴CD=nx,
∴DE2=CE2+CD2=n2x2+x2=(n2+1)x2,
∵BC2=n2x2,
∴![]() =
=![]() =
=![]() .
.


科目:初中数学 来源: 题型:
【题目】某校数学兴趣小组的成员小华对本班上学期期末考试数学成绩(成绩取整数,满分为100分)作了统计分析,绘制成如下频数分布表和频数分布直方图.

请你根据图表提供的信息,解答下列问题:
(1)频数分布表中a= ,b= ;
(2)补全频数分布直方图;
(3)数学老师准备从不低于90分的学生中选1人介绍学习经验,那么取得了93分的小华被选上的概率是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我省某地区为了了解2016年初中毕业生毕业去向,对部分九年级学生进行了抽样调查,就九年级学生毕业后的四种去向:A.读普通高中;B.读职业高中;C.直接进入社会就业;D.其他(如出国等)进行数据统计,并绘制了两幅不完整的统计图(如图1,如图2) 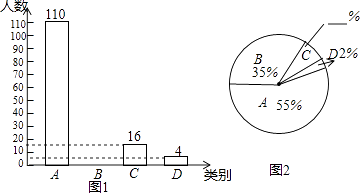
(1)填空:该地区共调查了 200 名九年级学生;
(2)将两幅统计图中不完整的部分补充完整;
(3)若该地区2016年初中毕业生共有3500人,请估计该地区今年初中毕业生中读普通高中的学生人数;
(4)老师想从甲,乙,丙,丁4位同学中随机选择两位同学了解他们毕业后的去向情况,请用画树状图或列表的方法求选中甲同学的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,分别以Rt△ABC的直角边AC及斜边AB向外作等边△ACD及等边△ABE,已知:∠BAC=30°,EF⊥AB,垂足为F,连接DF. 
(1)试说明AC=EF;
(2)求证:四边形ADFE是平行四边形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,O为坐标原点,四边形OABC为矩形,A(10,0),C(0,4),点D是OA中点,点P在BC上以每秒1个单位的速度由C向B运动,设运动时间为t秒.

(1)△ODP的面积S=________.
(2)t为何值时,四边形PODB是平行四边形?
(3)在线段PB上是否存在一点Q,使得ODQP为菱形?若存在,求t的值,并求出Q点的坐标;若不存在,请说明理由;
(4)若△OPD为等腰三角形,请写出所有满足条件的点P的坐标(请直接写出答案,不必写过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,抛物线y=ax2﹣ ![]() x+c经过原点O与点A(6,0)两点,过点A作AC⊥x轴,交直线y=2x﹣2于点C,且直线y=2x﹣2与x轴交于点D.
x+c经过原点O与点A(6,0)两点,过点A作AC⊥x轴,交直线y=2x﹣2于点C,且直线y=2x﹣2与x轴交于点D.
(1)求抛物线的解析式,并求出点C和点D的坐标;
(2)求点A关于直线y=2x﹣2的对称点A′的坐标,并判断点A′是否在抛物线上,并说明理由;
(3)点P(x,y)是抛物线上一动点,过点P作y轴的平行线,交线段CA′于点Q,设线段PQ的长为l,求l与x的函数关系式及l的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小丽购买学习用品的收据如表,因污损导致部分数据无法识别,根据下表,解决下列问题:
(1)小丽买了自动铅笔、记号笔各几支?
(2)若小丽再次购买软皮笔记本和自动铅笔两种文具,共花费15元,则有哪几种不同的购买方案?
商品名 | 单价(元) | 数量(个) | 金额(元) |
签字笔 | 3 | 2 | 6 |
自动铅笔 | 1.5 | ● | ● |
记号笔 | 4 | ● | ● |
软皮笔记本 | ● | 2 | 9 |
圆规 | 3.5 | 1 | ● |
合计 | 8 | 28 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com