
【题目】如图1,OABC的边OC在x轴的正半轴上,OC=5,反比例函数y= ![]() (x>0)的图象经过点A(1,4).
(x>0)的图象经过点A(1,4).
(1)求反比例函数的关系式和点B的坐标;
(2)如图2,过BC的中点D作DP∥x轴交反比例函数图象于点P,连接AP、OP.
①求△AOP的面积;
②在OABC的边上是否存在点M,使得△POM是以PO为斜边的直角三角形?若存在,请求出所有符合条件的点M的坐标;若不存在,请说明理由.
【答案】
(1)
解:∵反比例函数y= ![]() (x>0)的图象经过点A(1,4),
(x>0)的图象经过点A(1,4),
∴m=1×4=4,
∴反比例函数的关系式为y= ![]() (x>0).
(x>0).
∵四边形OABC为平行四边形,且点O(0,0),OC=5,点A(1,4),
∴点C(5,0),点B(6,4)
(2)
解:①延长DP交OA于点E,如图3所示.
∵点D为线段BC的中点,点C(5,0)、B(6,4),
∴点D( ![]() ,2).
,2).
令y= ![]() 中y=2,则x=2,
中y=2,则x=2,
∴点P(2,2),
∴PD= ![]() ﹣2=
﹣2= ![]() ,EP=ED﹣PD=
,EP=ED﹣PD= ![]() ,
,
∴S△AOP= ![]() EP(yA﹣yO)=
EP(yA﹣yO)= ![]() ×
× ![]() ×(4﹣0)=3.
×(4﹣0)=3.
②假设存在.以OP为直径作圆,交OC于点M1,交OA于点M2,连接PM1、PM2,如图4所示.
∵点P(2,2),O(0,0),
∴点M1(2,0);
∵点A(1,4),点O(0,0),
∴直线OA的关系式为y=4x.
设点M2(n,4n),
OM2= ![]() n,OP=2
n,OP=2 ![]() ,PM2=
,PM2= ![]() ,
,
∵∠OM2P=90°,
∴ ![]() +
+ ![]() =OP2,即17n2+17n2﹣20n+8=8,
=OP2,即17n2+17n2﹣20n+8=8,
解得:n= ![]() ,或n=0(舍去),
,或n=0(舍去),
∴点M2( ![]() ,
, ![]() ).
).
故在OABC的边上存在点M,使得△POM是以PO为斜边的直角三角形,点M的坐标为(2,0)或( ![]() ,
, ![]() ).
).


【解析】(1)由点A的坐标利用反比例函数图象上点的坐标特征即可求出反比例函数关系式,再根据平行四边形的性质结合点A、O、C的坐标即可求出点B的坐标;(2)①延长DP交OA于点E,由点D为线段BC的中点,可求出点D的坐标,再令反例函数关系式中y=2求出x值即可得出点P的坐标,由此即可得出PD、EP的长度,根据三角形的面积公式即可得出结论;②假设存在,以OP为直径作圆,交OC于点M1 , 交OA于点M2 , 通过解直角三角形和勾股定理求出点M1、M2的坐标,此题得解.本题考查了反比例函数图象上点的坐标特征、三角形的面积公式、平行四边形的性质以及解直角三角形,解题的关键是:(1)根据反比例函数图象上点的坐标特征求出反比例函数解析式;(2)①求出EP长度;②以OP为直径作圆,找出点M的位置.本题属于中档题,难度不大,解决该题型题目时,通过作圆来确定点的数目与位置是关键.
【考点精析】利用平行四边形的性质和解直角三角形对题目进行判断即可得到答案,需要熟知平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分;解直角三角形的依据:①边的关系a2+b2=c2;②角的关系:A+B=90°;③边角关系:三角函数的定义.(注意:尽量避免使用中间数据和除法).


科目:初中数学 来源: 题型:
【题目】为了倡导“节约用水,从我做起”的活动,某市政府决定对市直机关500户家庭的用水情况作一次调查,调查小组随机抽查了其中100户家庭一年的月平均用水量(单位:吨).并将调查结果制成了如图所示的条形统计图.
(1)求这100个样本数据的平均数、众数和中位数;
(2)根据样本数据,估计该市直机关500户家庭中月平均用水量不超过12吨的约有多少户?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校数学兴趣小组的成员小华对本班上学期期末考试数学成绩(成绩取整数,满分为100分)作了统计分析,绘制成如下频数分布表和频数分布直方图.

请你根据图表提供的信息,解答下列问题:
(1)频数分布表中a= ,b= ;
(2)补全频数分布直方图;
(3)数学老师准备从不低于90分的学生中选1人介绍学习经验,那么取得了93分的小华被选上的概率是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,AB=12,AD=8,∠ABC的平分线交CD于点F,交AD的延长线于点E,CG⊥BE,垂足为G,若EF=2,则线段CG的长为( ) 
A.![]()
B.4 ![]()
C.2 ![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】据图解答 
(1)如图1,在菱形ABCD中,CE=CF,求证:AE=AF.
(2)如图2,AB是⊙O的直径,PA与⊙O相切于点A,OP与⊙O相交于点C,连接CB,∠OPA=40°,求∠ABC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为2的正方形ABCD中剪去一个边长为1的小正方形CEFG,动点P从点A出发,沿A→D→E→F→G→B的路线绕多边形的边匀速运动到点B时停止(不含点A和点B),则△ABP的面积S随着时间t变化的函数图象大致是( )
A.
B.
C.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我省某地区为了了解2016年初中毕业生毕业去向,对部分九年级学生进行了抽样调查,就九年级学生毕业后的四种去向:A.读普通高中;B.读职业高中;C.直接进入社会就业;D.其他(如出国等)进行数据统计,并绘制了两幅不完整的统计图(如图1,如图2) 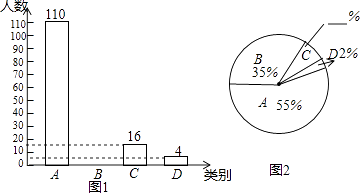
(1)填空:该地区共调查了 200 名九年级学生;
(2)将两幅统计图中不完整的部分补充完整;
(3)若该地区2016年初中毕业生共有3500人,请估计该地区今年初中毕业生中读普通高中的学生人数;
(4)老师想从甲,乙,丙,丁4位同学中随机选择两位同学了解他们毕业后的去向情况,请用画树状图或列表的方法求选中甲同学的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,分别以Rt△ABC的直角边AC及斜边AB向外作等边△ACD及等边△ABE,已知:∠BAC=30°,EF⊥AB,垂足为F,连接DF. 
(1)试说明AC=EF;
(2)求证:四边形ADFE是平行四边形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com