
科目:初中数学 来源: 题型:解答题
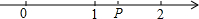 计算与化简:
计算与化简:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{3y}{5}$ | B. | $\frac{{a}^{2}b+1}{a{b}^{2}-1}$ | C. | $\frac{a+b}{(a+b)^{2}}$ | D. | $\frac{{a}^{2}+2a+1}{{a}^{2}-1}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
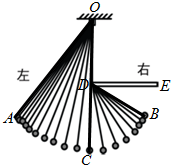 如图,一条细绳系着一个小球在平面内摆动.已知细绳从悬挂点O到球心的长度为50厘米,小球在A、B两个位置时达到最高点,且最高点高度相同(不计空气阻力),在C点位置时达到最低点.达到左侧最高点时与最低点时细绳相应所成的角度为37°,细绳在右侧达到最高点时与一个水平放置的挡板DE所成的角度为30°.(sin37°≈0.6,cos37°≈0.8,tan37°≈0.75)
如图,一条细绳系着一个小球在平面内摆动.已知细绳从悬挂点O到球心的长度为50厘米,小球在A、B两个位置时达到最高点,且最高点高度相同(不计空气阻力),在C点位置时达到最低点.达到左侧最高点时与最低点时细绳相应所成的角度为37°,细绳在右侧达到最高点时与一个水平放置的挡板DE所成的角度为30°.(sin37°≈0.6,cos37°≈0.8,tan37°≈0.75)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,△ABC中,AB=AC,BE=EC,直接使用“SSS”可判定( )
如图,△ABC中,AB=AC,BE=EC,直接使用“SSS”可判定( )| A. | △ABD≌△ACD | B. | △ABE≌△EDC | C. | △ABE≌△ACE | D. | △BED≌△CED |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
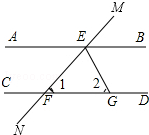 请补全说理过程:
请补全说理过程:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com