
【题目】如图,抛物线![]() 与
与![]() 交于点
交于点![]() ,过点
,过点![]() 作
作![]() 轴的平行线,分别交两条抛物线于点
轴的平行线,分别交两条抛物线于点![]() ,则以下结论:①无论
,则以下结论:①无论![]() 取何值,
取何值,![]() 的值总是正数;②
的值总是正数;②![]() ;③
;③![]() 其中正确结论是( )
其中正确结论是( )
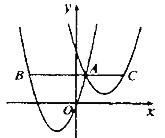
A. ①②B. ①③C. ②③D. 都正确
 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案科目:初中数学 来源: 题型:
【题目】已知二次函数y=kx2﹣(k+3)x+3图象的对称轴为:直线x=2.
(1)求该二次函数的表达式;
(2)画出该函数的图象,并结合图象直接写出:
①当y<0时,自变量x的取值范围;
②当0≤x<3时,y的取值范围是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形OABC的顶点A,C分别在x轴,y轴上,顶点B在第一象限,AB=1.将线段OA绕点O按逆时针方向旋转60°得到线段OP,连接AP,反比例函数![]() (k≠0)的图象经过P,B两点,则k的值为______________.
(k≠0)的图象经过P,B两点,则k的值为______________.
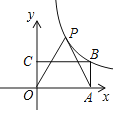
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() 三个顶点的坐标分别
三个顶点的坐标分别![]() .
.
(1)画出![]() ;
;
(2)以B为位似中心,将![]() 放大到原来的2倍,在右图的网格图中画出放大后的图形△
放大到原来的2倍,在右图的网格图中画出放大后的图形△![]() ;
;
(3)写出点A的对应点![]() 的坐标:___.
的坐标:___.
查看答案和解析>>
科目:初中数学 来源: 题型:
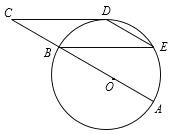
【题目】如图,⊙O的直径AB=12 cm,C为AB延长线上一点,CD与⊙O相切于点D,过点B作弦BE∥CD,连接DE.
(1)求证:点D为![]() 的中点;
的中点;
(2)若∠C=∠E,求四边形BCDE的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果关于x的一元二次方程ax2+bx+c=0 (a≠0)有两个不相等的实数根,且其中一个根为另一个根的2倍,那么称这样的方程为“倍根方程”.例如,方程x2-6x+8=0的两个根是2和4,则方程x2-6x+8=0就是“倍根方程”.
(1)若一元二次方程x2-3x+c=0是“倍根方程”,则c= ;
(2)若(x-2) (mx-n)=0(m≠0)是“倍根方程”,求代数式4m2-5mn+n2的值;
(3)若方程ax2+bx+c=0 (a≠0)是倍根方程,且相异两点M(1+t,s),N(4-t,s),都在抛物线y=ax2+bx+c上,求一元二次方程ax2+bx+c=0 (a≠0)的根.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】周老师家的红心猕猴桃深受广大顾客的喜爱,猕猴桃成熟上市后,她记录了15天的销售数量和销售单价,其中销售单价y(元/千克)与时间第x天(x为整数)的数量关系如图所示,日销量P(千克)与时间第x天(x为整数)的部分对应值如下表所示:
时间第x天 | 1 | 3 | 5 | 7 | 10 | 11 | 12 | 15 |
日销量P(千克) | 320 | 360 | 400 | 440 | 500 | 400 | 300 | 0 |
(1)求y与x的函数关系式,并写出自变量x的取值范围;
(2)从你学过的函数中,选择合适的函数类型刻画P随x的变化规律,请直接写出P与x的函数关系式及自变量x的取值范围;
(3)在这15天中,哪一天销售额达到最大,最大销售额是多少元;
(4)周老师非常热爱公益事业,若在前5天,周老师决定每销售1千克红心猕猴桃就捐献a元给“环保公益项目”,且希望每天的销售额不低于2800元以维持各种开支,求a的最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,AD⊥BC垂足是D,AN是∠BAC的外角∠CAM的平分线,CE⊥AN,垂足是E,连接DE交AC于F.
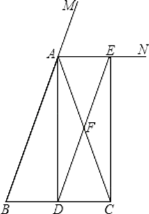
(1)求证:四边形ADCE为矩形;
(2)求证:DF∥AB,DF=![]() ;
;
(3)当△ABC满足什么条件时,四边形ADCE为正方形,简述你的理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com