
°Њћвƒњ°њ÷№јѕ ¶Љ“µƒЇм–ƒв®Їпћ“…о №єгіуєЋњЌµƒѕ≤∞Ѓ£ђв®Їпћ“≥… м…ѕ –Їу£ђЋэЉ«¬ЉЅЋ15ћмµƒѕъ џ эЅњЇЌѕъ џµ•Љџ£ђ∆д÷–ѕъ џµ•Љџy£®‘™/«ІњЋ£©”л ±ЉдµЏxћм£®xќ™’ы э£©µƒ эЅњєЎѕµ»зЌЉЋщ Њ£ђ»’ѕъЅњP£®«ІњЋ£©”л ±ЉдµЏxћм£®xќ™’ы э£©µƒ≤њЈ÷ґ‘”¶÷µ»зѕ¬±нЋщ Њ£Ї
±ЉдµЏxћм | 1 | 3 | 5 | 7 | 10 | 11 | 12 | 15 |
»’ѕъЅњP£®«ІњЋ£© | 320 | 360 | 400 | 440 | 500 | 400 | 300 | 0 |
£®1£©«уy”лxµƒЇѓ эєЎѕµ љ£ђ≤Ґ–і≥ц„‘±дЅњxµƒ»°÷µЈґќІ£ї
£®2£©і”ƒг—ІєэµƒЇѓ э÷–£ђ—°‘сЇѕ µƒЇѓ эја–Ќњћї≠PЋжxµƒ±дїѓєж¬…£ђ«л÷±љ”–і≥цP”лxµƒЇѓ эєЎѕµ љЉ∞„‘±дЅњxµƒ»°÷µЈґќІ£ї
£®3£©‘Џ’в15ћм÷–£ђƒƒ“їћмѕъ џґоіпµљ„оіу£ђ„оіуѕъ џґо «ґа…ў‘™£ї
£®4£©÷№јѕ ¶Ј«≥£»»∞ЃєЂ“ж ¬“µ£ђ»ф‘Џ«∞5ћм£ђ÷№јѕ ¶Њцґ®√њѕъ џ1«ІњЋЇм–ƒв®Їпћ“ЊЌЊиѕ„a‘™Єш°∞їЈ±£єЂ“жѕоƒњ°±£ђ«“ѕ£Ќы√њћмµƒѕъ џґо≤їµЌ”Џ2800‘™“‘ќђ≥÷Єч÷÷њ™÷І£ђ«уaµƒ„оіу÷µ.

°Њір∞Є°њ£®1£©![]() £®x»°’ы э£©£ї
£®x»°’ы э£©£ї
£®2£©![]() £®x»°’ы э£©£ї
£®x»°’ы э£©£ї
£®3£©µЏ10ћмѕъ џґоіпµљ„оіу£ђ„оіуѕъ џґо «4500‘™£ї
£®4£©![]() µƒ„оіу÷µќ™2
µƒ„оіу÷µќ™2
°Њљвќц°њ
£®1£©ЄщЊЁЇѓ эЌЉѕу£ђ”√іэґ®ѕµ эЈ®£ђЉіњ…«уµ√Їѓ эєЎѕµ љЉ∞∆д„‘±дЅњµƒЈґќІ£ї
£®2£©ЄщЊЁ±нЄсјпµƒЅљЄц±дЅњµƒ÷µ «Њщ‘»±дїѓµƒ£ђњ…÷™£ђp «єЎ”Џxµƒ“їіќЇѓ э£ђ”√іэґ®ѕµ эЈ®£ђЉіњ…«уµ√Їѓ э±ніп љЉ∞∆д„‘±дЅњµƒЈґќІ£ї
£®3£©ЄщЊЁ°∞√њћмµƒѕъ џґо=ѕъ џµ•Љџ°Ѕ»’ѕъ џЅњ°±£ђ‘Џ„‘±дЅњ![]() µƒ≤їЌђ»°÷µЈґќІƒЏ£ђњ…Ѕ–≥ц£ђѕъ џґоєЎ”Џ
µƒ≤їЌђ»°÷µЈґќІƒЏ£ђњ…Ѕ–≥ц£ђѕъ џґоєЎ”Џ![]() µƒЇѓ э±ніп љ£ђЈ÷±р«у≥цѕъ џґоµƒ„оіу÷µЉіњ…£ї
µƒЇѓ э±ніп љ£ђЈ÷±р«у≥цѕъ џґоµƒ„оіу÷µЉіњ…£ї
£®4£©ЄщЊЁћв“в£ђЅ–≥цєЎ”Џ![]() µƒ≤їµ» љ£ђ‘Џ
µƒ≤їµ» љ£ђ‘Џ![]() µƒ»°÷µЈґќІƒЏ£ђ«у≥ц≤ќ э
µƒ»°÷µЈґќІƒЏ£ђ«у≥ц≤ќ э![]() „оіу÷µЉіњ….
„оіу÷µЉіњ….
£®1£©Ґў µ±![]() ±£ђ…и
±£ђ…и![]() £®
£®![]() £©£ђ∞—µг£®0£ђ14£©£ђ£®5£ђ9£©іъ»л
£©£ђ∞—µг£®0£ђ14£©£ђ£®5£ђ9£©іъ»л![]() £ђµ√
£ђµ√![]() £ђљвµ√£Ї
£ђљвµ√£Ї![]() £ђ
£ђ
°а![]() £ї
£ї
ҐЏµ±![]() ±£ђ
±£ђ![]() £ђ
£ђ
°а![]() £®x»°’ы э£©£ї
£®x»°’ы э£©£ї
£®2£©”…±нЄс эЊЁњ…÷™£ђp «єЎ”Џxµƒ“їіќЇѓ э£ђ…и![]() £ђ
£ђ
Ґўµ±![]() ±£ђ∞—
±£ђ∞—![]() £ђіъ»лњ…µ√£Ї
£ђіъ»лњ…µ√£Ї![]() £ђ
£ђ
љвµ√£Ї![]() £ђ
£ђ
°а![]() £ї
£ї
ҐЏµ±![]() ±£ђЌђјн£ђ”√іэґ®ѕµ эЈ®њ…µ√£Ї
±£ђЌђјн£ђ”√іэґ®ѕµ эЈ®њ…µ√£Ї![]() £ђ
£ђ
°а![]() £®x»°’ы э£©£ї
£®x»°’ы э£©£ї
£®3£©…иѕъ џґоќ™![]() £ђ
£ђ
Ґўµ±![]() ±£ђ
±£ђ
![]() =
=![]() £ђ
£ђ
°аµ±![]() ±£ђ
±£ђ![]() £ї
£ї
ҐЏµ±![]() ±£ђ
±£ђ
![]() £ђ
£ђ
°аµ±![]() ±£ђ
±£ђ![]() £ї
£ї
Ґџµ±![]() ±£ђ
±£ђ![]() £ђ
£ђ
°аµ±![]() ±£ђ
±£ђ![]() £ђ
£ђ
„џ…ѕЋщ ц£ЇµЏ10ћмѕъ џґоіпµљ„оіу£ђ„оіуѕъ џґо «4500‘™£ї
£®4£©ЄщЊЁћв“в£ђњ…µ√£Ї
µ±![]() ±£ђ
±£ђ ![]() £ђ
£ђ
Љі![]() £ђ‘Џ
£ђ‘Џ![]() £ђ«“x»°’ы эЈґќІƒЏ£ђЇг≥…ЅҐ£ђ
£ђ«“x»°’ы эЈґќІƒЏ£ђЇг≥…ЅҐ£ђ
µ±x=1 ±£ђ![]() £ђљвµ√£Ї
£ђљвµ√£Ї![]() £ђ
£ђ
µ±x=2 ±£ђ![]() £ђљвµ√£Ї
£ђљвµ√£Ї![]() £ђ
£ђ
µ±x=3 ±£ђ![]() £ђљвµ√£Ї
£ђљвµ√£Ї![]() £ђ
£ђ
µ±x=4 ±£ђ![]() £ђљвµ√£Ї
£ђљвµ√£Ї![]() £ђ
£ђ
µ±x=5 ±£ђ![]() £ђљвµ√£Ї
£ђљвµ√£Ї![]() £ђ
£ђ
„џ…ѕЋщ ц£Ї![]() £ђ
£ђ
°а![]() µƒ„оіу÷µќ™2.
µƒ„оіу÷µќ™2.


 ∆я–«ЌЉ йњЏЋгЋўЋгћмћмЅЈѕµЅ–ір∞Є
∆я–«ЌЉ йњЏЋгЋўЋгћмћмЅЈѕµЅ–ір∞Є
| ƒкЉґ | Єя÷–њќ≥ћ | ƒкЉґ | ≥х÷–њќ≥ћ |
| Єя“ї | Єя“ї√вЈ—њќ≥ћЌ∆Љц£° | ≥х“ї | ≥х“ї√вЈ—њќ≥ћЌ∆Љц£° |
| Єяґю | Єяґю√вЈ—њќ≥ћЌ∆Љц£° | ≥хґю | ≥хґю√вЈ—њќ≥ћЌ∆Љц£° |
| Єя»э | Єя»э√вЈ—њќ≥ћЌ∆Љц£° | ≥х»э | ≥х»э√вЈ—њќ≥ћЌ∆Љц£° |
њ∆ƒњ£Ї≥х÷– э—І јі‘і£Ї ћв–Ќ£Ї
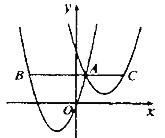
°Њћвƒњ°њ»зЌЉ£ђµгE «’эЈљ–ќABCDµƒ±яAB…ѕ“їµг£ђAB=4£ђDE=4.3£ђ°чDAEƒж ±’л–э„™Їуƒ№єї”л°чDCF÷ЎЇѕ£Ѓ

£®1£©–э„™÷––ƒ «______£ђ–э„™љ«ќ™______£ї
£®2£©«лƒг≈–ґѕ°чDFEµƒ–ќ„і£ђЉтµ•Ћµ√чјн”…£ї
£®3£©Ћƒ±я–ќDEBFµƒ√жїэќ™ £Ѓ
≤йњіір∞ЄЇЌљвќц>>
њ∆ƒњ£Ї≥х÷– э—І јі‘і£Ї ћв–Ќ£Ї
°Њћвƒњ°њ»зЌЉ£ђљЂ±я≥§ќ™8µƒ’эЈљ–ќ÷љ∆ђABCD—Ў„≈EF’џµю£ђ єµгC¬д‘ЏAB±яµƒ÷–µгMі¶£ЃµгD¬д‘ЏµгD'і¶£ђMD'”лADљї”ЏµгG£ђ‘т°чAMGµƒƒЏ«–‘≤∞лЊґµƒ≥§ќ™______.

≤йњіір∞ЄЇЌљвќц>>
њ∆ƒњ£Ї≥х÷– э—І јі‘і£Ї ћв–Ќ£Ї
°Њћвƒњ°њ»зЌЉ£ђ≈„ќпѕя![]() ”л
”л![]() љї”Џµг
љї”Џµг![]() £ђєэµг
£ђєэµг![]() „ч
„ч![]() ÷бµƒ∆љ––ѕя£ђЈ÷±рљїЅљћх≈„ќпѕя”Џµг
÷бµƒ∆љ––ѕя£ђЈ÷±рљїЅљћх≈„ќпѕя”Џµг![]() £ђ‘т“‘ѕ¬љб¬џ£ЇҐўќё¬џ
£ђ‘т“‘ѕ¬љб¬џ£ЇҐўќё¬џ![]() »°Їќ÷µ£ђ
»°Їќ÷µ£ђ![]() µƒ÷µ„№ «’э э£їҐЏ
µƒ÷µ„№ «’э э£їҐЏ![]() £їҐџ
£їҐџ![]() ∆д÷–’э»Јљб¬џ «£® £©
∆д÷–’э»Јљб¬џ «£® £©
A. ҐўҐЏB. ҐўҐџC. ҐЏҐџD. ґЉ’э»Ј
≤йњіір∞ЄЇЌљвќц>>
њ∆ƒњ£Ї≥х÷– э—І јі‘і£Ї ћв–Ќ£Ї
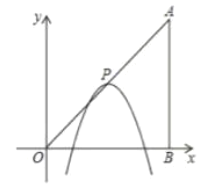
°Њћвƒњ°њ»зЌЉ£ђ‘Џ∆љ√ж÷±љ«„ш±кѕµ÷–£ђµг![]() £ђ
£ђ![]() µƒ„ш±кЈ÷±рќ™
µƒ„ш±кЈ÷±рќ™![]() £ђ
£ђ![]() £ђ≈„ќпѕя
£ђ≈„ќпѕя![]() µƒґ•µг
µƒґ•µг![]() ‘Џ’џѕя
‘Џ’џѕя![]() …ѕ‘Ћґѓ.
…ѕ‘Ћґѓ.
£®1£©µ±µг![]() ‘Џѕяґќ
‘Џѕяґќ![]() …ѕ‘Ћґѓ ±£ђ≈„ќпѕя
…ѕ‘Ћґѓ ±£ђ≈„ќпѕя![]() ”л
”л![]() ÷бљїµг„ш±кќ™
÷бљїµг„ш±кќ™![]() .
.
Ґў”√Їђ![]() µƒіъ э љ±н Њ
µƒіъ э љ±н Њ![]() .
.
ҐЏ«у![]() µƒ»°÷µЈґќІ.
µƒ»°÷µЈґќІ.
£®2£©µ±≈„ќпѕя”л![]() µƒ±я”–»эЄцєЂє≤µг ±£ђ ‘«у≥цµг
µƒ±я”–»эЄцєЂє≤µг ±£ђ ‘«у≥цµг![]() µƒ„ш±к.
µƒ„ш±к.
≤йњіір∞ЄЇЌљвќц>>
њ∆ƒњ£Ї≥х÷– э—І јі‘і£Ї ћв–Ќ£Ї
°Њћвƒњ°њ‘Џ°чABC÷–£ђ»фOќ™BC±яµƒ÷–µг£ђ‘т±Ў”–£ЇAB2£ЂAC2£љ2AO2£Ђ2BO2≥…ЅҐ£Ѓ“јЊЁ“‘…ѕљб¬џ£ђљвЊц»зѕ¬ќ ћв£Ї»зЌЉ£ђ‘ЏЊЎ–ќDEFG÷–£ђ“—÷™DE£љ4£ђEF£љ3£ђµгP‘Џ“‘DEќ™÷±Њґµƒ∞л‘≤…ѕ‘Ћґѓ£ђ‘т![]() µƒ„о–°÷µќ™________£Ѓ
µƒ„о–°÷µќ™________£Ѓ

≤йњіір∞ЄЇЌљвќц>>
њ∆ƒњ£Ї≥х÷– э—І јі‘і£Ї ћв–Ќ£Ї
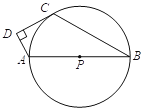
°Њћвƒњ°њ»зЌЉ£ђ“—÷™AB «°—Pµƒ÷±Њґ£ђµг![]() ‘Џ°—P…ѕ£ђ
‘Џ°—P…ѕ£ђ![]() ќ™°—PЌв“їµг£ђ«“°ѕADC£љ90°г£ђ÷±ѕя
ќ™°—PЌв“їµг£ђ«“°ѕADC£љ90°г£ђ÷±ѕя![]() ќ™°—Pµƒ«–ѕя£Ѓ
ќ™°—Pµƒ«–ѕя£Ѓ
Ґ≈ ‘Ћµ√ч£Ї2°ѕB£Ђ°ѕDAB£љ180°г
Ґ∆ »ф°ѕB£љ30°г£ђAD£љ2£ђ«у°—Pµƒ∞лЊґ£Ѓ
≤йњіір∞ЄЇЌљвќц>>
њ∆ƒњ£Ї≥х÷– э—І јі‘і£Ї ћв–Ќ£Ї
°Њћвƒњ°њ“—÷™£Ї°—Oµƒ∞лЊґќ™13cm£ђѕ“AB=24cm£ђѕ“CD=10cm£ђAB//CD£Ѓ‘т’вЅљћх∆љ––ѕ“AB£ђCD÷ЃЉдµƒЊајл « ________________
≤йњіір∞ЄЇЌљвќц>>
њ∆ƒњ£Ї≥х÷– э—І јі‘і£Ї ћв–Ќ£Ї
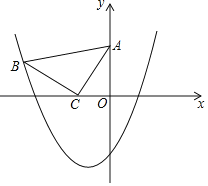
°Њћвƒњ°њ»зЌЉЋщ Њ£ђ‘Џ∆љ√ж÷±љ«„ш±кѕµxOy÷–£ђ”–ABќ™–±±яµƒµ»—ь÷±љ«»эљ«–ќABC£ђ∆д÷–µгA£®0£ђ2£©£ђµгC£®©Б1£ђ0£©£ђ≈„ќпѕяy£љax2+ax©Б2Њ≠єэBµг£Ѓ
£®1£©«уBµгµƒ„ш±к£ї
£®2£©«у≈„ќпѕяµƒљвќц љ£ї
£®3£©‘Џ≈„ќпѕя…ѕ «Јсіж‘ЏµгN£®µгB≥эЌв£©£ђ єµ√°чACN»‘»ї «“‘ACќ™÷±љ«±яµƒµ»—ь÷±љ«»эљ«–ќ£њ»фіж‘Џ£ђ«уµгNµƒ„ш±к£ї»ф≤їіж‘Џ£ђ«лЋµ√чјн”…£Ѓ
≤йњіір∞ЄЇЌљвќц>>
єъЉ —І–£”≈—° - ЅЈѕ∞≤бЅ–±н - ‘ћвЅ–±н
Їю±± °ї•Ѕ™Ќшќ•Ј®ЇЌ≤їЅЉ–≈ѕҐЊў±®∆љћ® | Ќш…ѕ”–Ї¶–≈ѕҐЊў±®„®«ш | µз–≈’©∆≠Њў±®„®«ш | …жјъ Ј–йќё÷ч“е”–Ї¶–≈ѕҐЊў±®„®«ш | …ж∆у«÷»®Њў±®„®«ш
ќ•Ј®ЇЌ≤їЅЉ–≈ѕҐЊў±®µзї∞£Ї027-86699610 Њў±®” ѕд£Ї58377363@163.com