
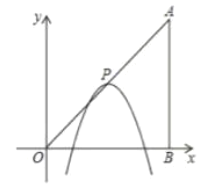
【题目】如图,在平面直角坐标系中,点![]() ,
,![]() 的坐标分别为
的坐标分别为![]() ,
,![]() ,抛物线
,抛物线![]() 的顶点
的顶点![]() 在折线
在折线![]() 上运动.
上运动.
(1)当点![]() 在线段
在线段![]() 上运动时,抛物线
上运动时,抛物线![]() 与
与![]() 轴交点坐标为
轴交点坐标为![]() .
.
①用含![]() 的代数式表示
的代数式表示![]() .
.
②求![]() 的取值范围.
的取值范围.
(2)当抛物线与![]() 的边有三个公共点时,试求出点
的边有三个公共点时,试求出点![]() 的坐标.
的坐标.
【答案】(1)①n=m;②![]() ;(2)
;(2)![]() 或
或![]() 或
或![]()
【解析】
(1)①设直线OA的解析式为y=kx,把点(6,6)代入可得k=1,推出y=x.因为y=-(x-m)2+n的顶点P在OA上,推出n=m.②由题意:y=-x2+2mx-m2+m,由抛物线与y轴交点坐标为(0,c),推出c=-m2+m,根据0≤m≤6,利用二次函数的性质即可解决问题;
(2)分三种情形①当抛物线经过点O时,抛物线与△ABO的边有三个公共点,
②当抛物线经过点A时,抛物线与△ABO的边有三个公共点,此时P(6,6);
③当点P在AB上运动,抛物线与OA只有一个公共点时,抛物线与△ABO的边有三个公共点.
解:(1)①设直线![]() 的解析式为
的解析式为![]() ,
,
∵经过![]()
∴![]()
∴![]()
∴![]()
∵![]() 的顶点
的顶点![]() 在
在![]() 上
上
∴![]()
②由题意:![]()
∵抛物线与![]() 轴交点坐标为
轴交点坐标为![]()
∴![]()
∵点![]() 在线段
在线段![]() 上,
上,
∴![]() ,
,![]()
∵![]()
∴当![]() 时,
时,![]()
当![]() 时,
时,![]()
∴![]() 的取值范围为
的取值范围为![]()
(2)①当抛物线经过点![]() 时,抛物线与
时,抛物线与![]() 的边有三个公共点,
的边有三个公共点,
把![]() 代入抛物线
代入抛物线![]() ,得到
,得到![]() 或0(舍弃),此时
或0(舍弃),此时![]()
②当抛物线经过点![]() 时,抛物线与
时,抛物线与![]() 的边有三个公共点,此时
的边有三个公共点,此时![]() .
.
③当点![]() 在
在![]() 上运动,抛物线与
上运动,抛物线与![]() 只有一个公共点时,抛物线与
只有一个公共点时,抛物线与![]() 的边有三个公共点,
的边有三个公共点,
由 ,消去
,消去![]() 得到
得到![]()
由题意![]() ,∴
,∴![]()
∴![]()
∴![]()
综上所述,满足条件的点![]() 坐标为
坐标为![]() 或
或![]() 或
或![]()


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
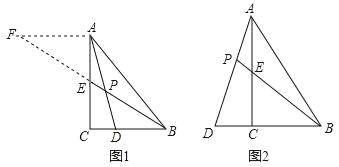
【题目】在△ABC中,∠ACB=90°,BE是AC边上的中线,点D在射线BC上.
发现:如图1,点D在BC边上,CD:BD=1:2,AD与BE相交于点P,过点A作AF∥BC,交BE的延长线于点F,求![]() 的值为.
的值为.
解决问题:如图2,在△ABC中,∠ACB=90°,点D在BC的延长线上,AD与AC边上的中线BE的延长线交于点P,DC:BC=1:2.求![]() 的值.
的值.
应用:若CD=2,AC=6,求BP的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O的直径AB=12 cm,C为AB延长线上一点,CD与⊙O相切于点D,过点B作弦BE∥CD,连接DE.
(1)求证:点D为![]() 的中点;
的中点;
(2)若∠C=∠E,求四边形BCDE的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】沙坪坝区各街道居民积极响应“创文明城区”活动,据了解,某街道居民人口共有7.5万人,街道划分为A,B两个社区,B社区居民人口数量不超过A社区居民人口数量的2倍.
(1)求A社区居民人口至少有多少万人?
(2)街道工作人员调查A,B两个社区居民对“社会主义核心价值观”知晓情况发现:A社区有1.2万人知晓,B社区有1.5万人知晓,为了提高知晓率,街道工作人员用了两个月的时间加强宣传,A社区的知晓人数平均月增长率为m%,B社区的知晓人数第一个月增长了![]() m%,第二月在第一个月的基础上又增长了2m%,两个月后,街道居民的知晓率达到92%,求m的值.
m%,第二月在第一个月的基础上又增长了2m%,两个月后,街道居民的知晓率达到92%,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】周老师家的红心猕猴桃深受广大顾客的喜爱,猕猴桃成熟上市后,她记录了15天的销售数量和销售单价,其中销售单价y(元/千克)与时间第x天(x为整数)的数量关系如图所示,日销量P(千克)与时间第x天(x为整数)的部分对应值如下表所示:
时间第x天 | 1 | 3 | 5 | 7 | 10 | 11 | 12 | 15 |
日销量P(千克) | 320 | 360 | 400 | 440 | 500 | 400 | 300 | 0 |
(1)求y与x的函数关系式,并写出自变量x的取值范围;
(2)从你学过的函数中,选择合适的函数类型刻画P随x的变化规律,请直接写出P与x的函数关系式及自变量x的取值范围;
(3)在这15天中,哪一天销售额达到最大,最大销售额是多少元;
(4)周老师非常热爱公益事业,若在前5天,周老师决定每销售1千克红心猕猴桃就捐献a元给“环保公益项目”,且希望每天的销售额不低于2800元以维持各种开支,求a的最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
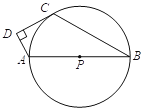
【题目】如图,已知AB是⊙P的直径,点![]() 在⊙P上,
在⊙P上,![]() 为⊙P外一点,且∠ADC=90°,直线
为⊙P外一点,且∠ADC=90°,直线![]() 为⊙P的切线.
为⊙P的切线.
⑴ 试说明:2∠B+∠DAB=180°
⑵ 若∠B=30°,AD=2,求⊙P的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于x 的一元二次方程a x2 + bx + c = 0(a>0)有两个不相等且非零的实数根,探究a,b,c满足的条件.
小华根据学习函数的经验,认为可以从二次函数的角度看一元二次方程,下面是小华的探究过程:第一步:设一元二次方程ax2 +bx+c = 0(a>0)对应的二次函数为y = ax2 +bx +c(a>0);
第二步:借助二次函数图象,可以得到相应的一元二次方程中a,b,c满足的条件,列表如下:
方程两根的情况 | 对应的二次函数的大致图象 | a,b,c满足的条件 |
方程有两个 不相等的负实根 |
|
|
①_______ |
|
|
方程有两个 不相等的正实根 | ②__________ | ③____________ |
(1)请帮助小华将上述表格补充完整;
(2)参考小华的做法,解决问题:
若关于x的一元二次方程![]() 有一个负实根和一个正实根,且负实根大于-1,求实数
有一个负实根和一个正实根,且负实根大于-1,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(定义[a,b,c]为函数![]() 的特征数,下面给出特征数为 [2m,1-m,-1-m]的函数的一些结论:
的特征数,下面给出特征数为 [2m,1-m,-1-m]的函数的一些结论:
①当m=-3时,函数图象的顶点坐标是(![]() ,
,![]() );
);
②当m>0时,函数图象截x轴所得的线段长度大于![]() ;
;
③当m<0时,函数在![]() 时,y随x的增大而减小;
时,y随x的增大而减小;
④当m≠0时,函数图象经过x轴上一个定点.
其中正确的结论有________ .(只需填写序号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com