
【题目】如图,将边长为8的正方形纸片ABCD沿着EF折叠,使点C落在AB边的中点M处.点D落在点D'处,MD'与AD交于点G,则△AMG的内切圆半径的长为______.

 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】某校九年级(1)班部分学生接受一次内容为“最适合自己的考前减压方式”的调查活动,收集整理数据后,老师将减压方式分为五类,并绘制了如图①②两幅不完整的统计图,请根据图中的信息解答下列问题.
(1)九年级(1)班接受调查的学生共有多少名?
(2)补全条形统计图,并计算扇形统计图中的“体育活动C”所对应的圆心角度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市销售一种牛奶,进价为每箱24元,规定售价不低于进价.现在的售价为每箱36元,每月可销售60箱.市场调查发现:若这种牛奶的售价每降价1元,则每月的销量将增加10箱,设每箱牛奶降价x元(x为正整数),每月的销量为y箱.
(1)写出y与x中间的函数关系式和自变量![]() 的取值范围;
的取值范围;
(2)超市如何定价,才能使每月销售牛奶的利润最大?最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
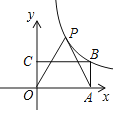
【题目】如图,矩形OABC的顶点A,C分别在x轴,y轴上,顶点B在第一象限,AB=1.将线段OA绕点O按逆时针方向旋转60°得到线段OP,连接AP,反比例函数![]() (k≠0)的图象经过P,B两点,则k的值为______________.
(k≠0)的图象经过P,B两点,则k的值为______________.
查看答案和解析>>
科目:初中数学 来源: 题型:
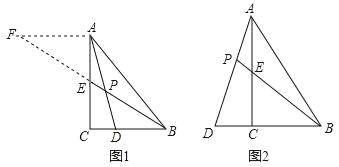
【题目】在△ABC中,∠ACB=90°,BE是AC边上的中线,点D在射线BC上.
发现:如图1,点D在BC边上,CD:BD=1:2,AD与BE相交于点P,过点A作AF∥BC,交BE的延长线于点F,求![]() 的值为.
的值为.
解决问题:如图2,在△ABC中,∠ACB=90°,点D在BC的延长线上,AD与AC边上的中线BE的延长线交于点P,DC:BC=1:2.求![]() 的值.
的值.
应用:若CD=2,AC=6,求BP的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() 三个顶点的坐标分别
三个顶点的坐标分别![]() .
.
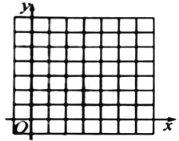
(1)画出![]() ;
;
(2)以B为位似中心,将![]() 放大到原来的2倍,在右图的网格图中画出放大后的图形△
放大到原来的2倍,在右图的网格图中画出放大后的图形△![]() ;
;
(3)写出点A的对应点![]() 的坐标:___.
的坐标:___.
查看答案和解析>>
科目:初中数学 来源: 题型:
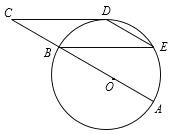
【题目】如图,⊙O的直径AB=12 cm,C为AB延长线上一点,CD与⊙O相切于点D,过点B作弦BE∥CD,连接DE.
(1)求证:点D为![]() 的中点;
的中点;
(2)若∠C=∠E,求四边形BCDE的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】周老师家的红心猕猴桃深受广大顾客的喜爱,猕猴桃成熟上市后,她记录了15天的销售数量和销售单价,其中销售单价y(元/千克)与时间第x天(x为整数)的数量关系如图所示,日销量P(千克)与时间第x天(x为整数)的部分对应值如下表所示:
时间第x天 | 1 | 3 | 5 | 7 | 10 | 11 | 12 | 15 |
日销量P(千克) | 320 | 360 | 400 | 440 | 500 | 400 | 300 | 0 |
(1)求y与x的函数关系式,并写出自变量x的取值范围;
(2)从你学过的函数中,选择合适的函数类型刻画P随x的变化规律,请直接写出P与x的函数关系式及自变量x的取值范围;
(3)在这15天中,哪一天销售额达到最大,最大销售额是多少元;
(4)周老师非常热爱公益事业,若在前5天,周老师决定每销售1千克红心猕猴桃就捐献a元给“环保公益项目”,且希望每天的销售额不低于2800元以维持各种开支,求a的最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知等边三角形ABC,O为△ABC内一点,连接OA,OB,OC,将△BAO绕点B旋转至△BCM.
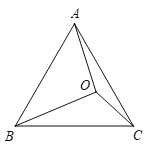
(1)依题意补全图形;
(2)若OA=![]() ,OB=
,OB=![]() ,OC=1,求∠OCM的度数.
,OC=1,求∠OCM的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com