
【题目】已知:⊙O的半径为13cm,弦AB=24cm,弦CD=10cm,AB//CD.则这两条平行弦AB,CD之间的距离是 ________________
科目:初中数学 来源: 题型:
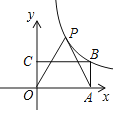
【题目】如图,矩形OABC的顶点A,C分别在x轴,y轴上,顶点B在第一象限,AB=1.将线段OA绕点O按逆时针方向旋转60°得到线段OP,连接AP,反比例函数![]() (k≠0)的图象经过P,B两点,则k的值为______________.
(k≠0)的图象经过P,B两点,则k的值为______________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】周老师家的红心猕猴桃深受广大顾客的喜爱,猕猴桃成熟上市后,她记录了15天的销售数量和销售单价,其中销售单价y(元/千克)与时间第x天(x为整数)的数量关系如图所示,日销量P(千克)与时间第x天(x为整数)的部分对应值如下表所示:
时间第x天 | 1 | 3 | 5 | 7 | 10 | 11 | 12 | 15 |
日销量P(千克) | 320 | 360 | 400 | 440 | 500 | 400 | 300 | 0 |
(1)求y与x的函数关系式,并写出自变量x的取值范围;
(2)从你学过的函数中,选择合适的函数类型刻画P随x的变化规律,请直接写出P与x的函数关系式及自变量x的取值范围;
(3)在这15天中,哪一天销售额达到最大,最大销售额是多少元;
(4)周老师非常热爱公益事业,若在前5天,周老师决定每销售1千克红心猕猴桃就捐献a元给“环保公益项目”,且希望每天的销售额不低于2800元以维持各种开支,求a的最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于x 的一元二次方程a x2 + bx + c = 0(a>0)有两个不相等且非零的实数根,探究a,b,c满足的条件.
小华根据学习函数的经验,认为可以从二次函数的角度看一元二次方程,下面是小华的探究过程:第一步:设一元二次方程ax2 +bx+c = 0(a>0)对应的二次函数为y = ax2 +bx +c(a>0);
第二步:借助二次函数图象,可以得到相应的一元二次方程中a,b,c满足的条件,列表如下:
方程两根的情况 | 对应的二次函数的大致图象 | a,b,c满足的条件 |
方程有两个 不相等的负实根 |
|
|
①_______ |
|
|
方程有两个 不相等的正实根 | ②__________ | ③____________ |
(1)请帮助小华将上述表格补充完整;
(2)参考小华的做法,解决问题:
若关于x的一元二次方程![]() 有一个负实根和一个正实根,且负实根大于-1,求实数
有一个负实根和一个正实根,且负实根大于-1,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
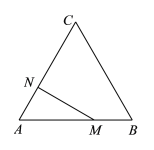
【题目】如图,等边△ABC的边长为3cm,点N在AC边上,AN=1cm.△ABC边上的动点M从点A出发,沿A→B→C运动,到达点C时停止.设点M运动的路程为xcm,MN的长为ycm.
小西根据学习函数的经验,对函数y随自变量x的变化而变化的规律进行了探究.
下面是小西的探究过程,请补充完整:
(1)通过取点、画图、测量,得到了y与x的几组对应值;
x/cm | 0 | 0.5 | 1 | 1.5 | 2 | 2.5 | 3 | 3.5 | 4 | 4.5 | 5 | 5.5 | 6 |
y/cm | 1 | 0.87 | 1 | 1.32 | 2.18 | 2.65 | 2.29 | 1.8 | 1.73 | 1.8 | 2 |
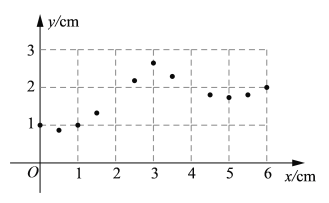
(2)在平面直角坐标系![]() 中,描出补全后的表中各组数值所对应的点,画出该函数的图象;
中,描出补全后的表中各组数值所对应的点,画出该函数的图象;
(3) 结合函数图象,解决问题:当MN=2cm时,点M运动的路程为 cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知等边三角形ABC,O为△ABC内一点,连接OA,OB,OC,将△BAO绕点B旋转至△BCM.
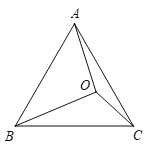
(1)依题意补全图形;
(2)若OA=![]() ,OB=
,OB=![]() ,OC=1,求∠OCM的度数.
,OC=1,求∠OCM的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,AD⊥BC垂足是D,AN是∠BAC的外角∠CAM的平分线,CE⊥AN,垂足是E,连接DE交AC于F.
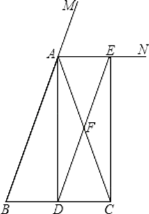
(1)求证:四边形ADCE为矩形;
(2)求证:DF∥AB,DF=![]() ;
;
(3)当△ABC满足什么条件时,四边形ADCE为正方形,简述你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 与
与![]() 轴、
轴、![]() 轴分别交于
轴分别交于![]() 两点,抛物线
两点,抛物线![]() 经过点
经过点![]() ,与
,与![]() 轴另一交点为
轴另一交点为![]() ,顶点为
,顶点为![]() .
.
(1)求抛物线的解析式;
(2)在![]() 轴上找一点
轴上找一点![]() ,使
,使![]() 的值最小,求
的值最小,求![]() 的最小值;
的最小值;
(3)在抛物线的对称轴上是否存在一点![]() ,使得
,使得![]() ?若存在,求出
?若存在,求出![]() 点坐标;若不存在,请说明理由.
点坐标;若不存在,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com