
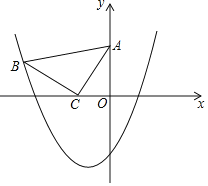
【题目】如图所示,在平面直角坐标系xOy中,有AB为斜边的等腰直角三角形ABC,其中点A(0,2),点C(﹣1,0),抛物线y=ax2+ax﹣2经过B点.
(1)求B点的坐标;
(2)求抛物线的解析式;
(3)在抛物线上是否存在点N(点B除外),使得△ACN仍然是以AC为直角边的等腰直角三角形?若存在,求点N的坐标;若不存在,请说明理由.
【答案】(1)(﹣3,1) (2)y=![]() x2+
x2+![]() x﹣2 (3)见解析
x﹣2 (3)见解析
【解析】
(1)根据题意,过点B作BD⊥x轴,垂足为D;根据角的互余的关系,易得B到x、y轴的距离,即B的坐标;
(2)根据抛物线过B点的坐标,可得a的值,进而可得其解析式;
(3)首先假设存在,分A、C是直角顶点两种情况讨论,根据全等三角形的性质,可得答案.
解:(1)过点B作BD⊥x轴,垂足为D.
∵∠BCD+∠ACO=90°,∠ACO+∠CAO=90°,
∴∠BCD=∠CAO,
又∵∠BDC=∠COA=90°,CB=AC,
∴△BCD≌△CAO,
∴BD=OC=1,CD=OA=2,
∴点B的坐标为(﹣3,1);
(2)抛物线y=ax2+ax﹣2经过点B(﹣3,1),
则得到1=9a﹣3a﹣2,
解得a=![]() ,
,
所以抛物线的解析式为y=![]() x2+
x2+![]() x﹣2;
x﹣2;
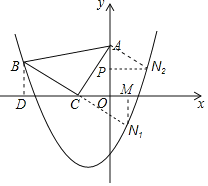
(3)假设存在点N,使得△ACN仍然是以AC为直角边的等腰直角三角形:
①若以点C为直角顶点;
则延长BC至点N1,使得N1C=BC,得到等腰直角三角形△ACN1,
过点N1作N1M⊥x轴,
∵CN1=BC,∠MCN1=∠BCD,∠N1MC=∠BDC=90°,
∴△MN1C≌△DBC.
∴CM=CD=2,N1M=BD=1,可求得点N1(1,﹣1);
②若以点A为直角顶点;
则过点A作AN2⊥CA,且使得AN2=AC,得到等腰直角三角形△ACN2,
过点N2作N2P⊥y轴,同理可证△AN2P≌△CAO,
∴NP2=OA=2,AP=OC=1,可求得点N2(2,1),
③以A为直角顶点的等腰Rt△ACN的顶点N有两种情况.即过点A作直线L⊥AC,在直线L上截取AN=AC时,点N可能在y轴右侧,即现在解答情况②的点N2;
点N也可能在y轴左侧,即还有第③种情况的点N3.因此,然后过N3作N3G⊥y轴于G,同理:△AGN3≌△CAO,
∴GN3=OA=2,AG=OC=1,
∴N3(﹣2,3);
经检验,点N1(1,﹣1)与点N2(2,1)都在抛物线y=![]() x2+
x2+![]() x﹣2上,点N3(﹣2,3)不在抛物线上.
x﹣2上,点N3(﹣2,3)不在抛物线上.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】周老师家的红心猕猴桃深受广大顾客的喜爱,猕猴桃成熟上市后,她记录了15天的销售数量和销售单价,其中销售单价y(元/千克)与时间第x天(x为整数)的数量关系如图所示,日销量P(千克)与时间第x天(x为整数)的部分对应值如下表所示:
时间第x天 | 1 | 3 | 5 | 7 | 10 | 11 | 12 | 15 |
日销量P(千克) | 320 | 360 | 400 | 440 | 500 | 400 | 300 | 0 |
(1)求y与x的函数关系式,并写出自变量x的取值范围;
(2)从你学过的函数中,选择合适的函数类型刻画P随x的变化规律,请直接写出P与x的函数关系式及自变量x的取值范围;
(3)在这15天中,哪一天销售额达到最大,最大销售额是多少元;
(4)周老师非常热爱公益事业,若在前5天,周老师决定每销售1千克红心猕猴桃就捐献a元给“环保公益项目”,且希望每天的销售额不低于2800元以维持各种开支,求a的最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知等边三角形ABC,O为△ABC内一点,连接OA,OB,OC,将△BAO绕点B旋转至△BCM.
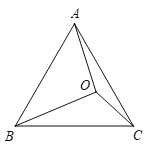
(1)依题意补全图形;
(2)若OA=![]() ,OB=
,OB=![]() ,OC=1,求∠OCM的度数.
,OC=1,求∠OCM的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,AD⊥BC垂足是D,AN是∠BAC的外角∠CAM的平分线,CE⊥AN,垂足是E,连接DE交AC于F.
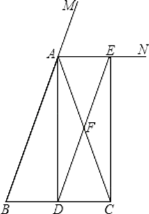
(1)求证:四边形ADCE为矩形;
(2)求证:DF∥AB,DF=![]() ;
;
(3)当△ABC满足什么条件时,四边形ADCE为正方形,简述你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(定义[a,b,c]为函数![]() 的特征数,下面给出特征数为 [2m,1-m,-1-m]的函数的一些结论:
的特征数,下面给出特征数为 [2m,1-m,-1-m]的函数的一些结论:
①当m=-3时,函数图象的顶点坐标是(![]() ,
,![]() );
);
②当m>0时,函数图象截x轴所得的线段长度大于![]() ;
;
③当m<0时,函数在![]() 时,y随x的增大而减小;
时,y随x的增大而减小;
④当m≠0时,函数图象经过x轴上一个定点.
其中正确的结论有________ .(只需填写序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商品的进价为每件20元,售价为每件30元,每月可卖出180件,如果该商品计划涨价销售,但每件售价不能高于35元,设每件商品的售价上涨x元(x为整数)时,月销售利润为y元.
(1)分析数量关系填表:
每台售价(元) | 30 | 31 | 32 | …… | 30+x |
月销售量(件) | 180 | 170 | 160 | …… | _____ |
(2)求y与x之间的函数解析式和x的取值范围
(3)当售价x(元/件)定为多少时,商场每月销售这种商品所获得的利润y(元)最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,△ABC是等边三角形,点D、E分别在边BC、AC上,∠ADE=60°.
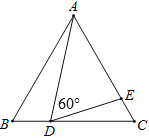
(1)求证:△ABD∽△DCE;
(2)如果AB=3,EC=![]() ,求DC的长.
,求DC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 与
与![]() 轴、
轴、![]() 轴分别交于
轴分别交于![]() 两点,抛物线
两点,抛物线![]() 经过点
经过点![]() ,与
,与![]() 轴另一交点为
轴另一交点为![]() ,顶点为
,顶点为![]() .
.
(1)求抛物线的解析式;
(2)在![]() 轴上找一点
轴上找一点![]() ,使
,使![]() 的值最小,求
的值最小,求![]() 的最小值;
的最小值;
(3)在抛物线的对称轴上是否存在一点![]() ,使得
,使得![]() ?若存在,求出
?若存在,求出![]() 点坐标;若不存在,请说明理由.
点坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,AB=4,AC与BD交于点O, N是AO的中点,点M在BC边上,且BM=3, P为对角线BD上一点,当对角线BD平分∠NPM时,PM-PN值为( )

A.1B.![]() C.2D.
C.2D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com