
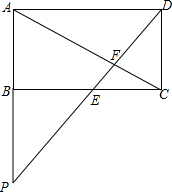
 如图,已知四边形ABCD是矩形,求证:DF2=EF•FP.
如图,已知四边形ABCD是矩形,求证:DF2=EF•FP. 分析 由四边形ABCD是矩形,得到AD∥BC,AB∥CD,求得△ADF∽△CEF,△CDF∽△APF,根据相似三角形的性质得到$\frac{DF}{PF}=\frac{CF}{AF}$,$\frac{EF}{DF}=\frac{CF}{AF}$,等量代换即可得到结论.
解答 解:∵四边形ABCD是矩形,
∴AD∥BC,AB∥CD,
∴△ADF∽△CEF,△CDF∽△APF,
∴$\frac{DF}{PF}=\frac{CF}{AF}$,$\frac{EF}{DF}=\frac{CF}{AF}$,
∴$\frac{DF}{PF}=\frac{EF}{DF}$,
∴DF2=EF•FP.
点评 本题考查了相似三角形的判定和性质,矩形的性质,熟练掌握相似三角形的判定和性质是解题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
 如图,在Rt△ABC中,∠ACB=90°,AB=6,若以AB边和BC边向外作等腰直角三角形AFC和等腰直角三角形BEC.若△BEC的面积为S1,△AFC的面积为S2,则S1+S2=( )
如图,在Rt△ABC中,∠ACB=90°,AB=6,若以AB边和BC边向外作等腰直角三角形AFC和等腰直角三角形BEC.若△BEC的面积为S1,△AFC的面积为S2,则S1+S2=( )| A. | 4 | B. | 9 | C. | 18 | D. | 36 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 为响应市委市政府提出的建设“绿色荆州”的号召,我市某单位准备将院内一块长30m,宽20m的长方形空地建成一个矩形花园,要求在花园中修两条纵向平行和一条横向弯折的小道,剩余的地方种植花草.如图所示,要使种植花草的面积为532m2,那么小道进出口的宽度应为多少米?(注:所有小道进出口的宽度相等,且每段小道均为平行四边形)则小道进出口的宽度为1米.
为响应市委市政府提出的建设“绿色荆州”的号召,我市某单位准备将院内一块长30m,宽20m的长方形空地建成一个矩形花园,要求在花园中修两条纵向平行和一条横向弯折的小道,剩余的地方种植花草.如图所示,要使种植花草的面积为532m2,那么小道进出口的宽度应为多少米?(注:所有小道进出口的宽度相等,且每段小道均为平行四边形)则小道进出口的宽度为1米.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
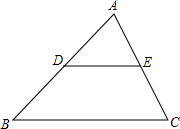 如图,在△ABC中,点D,E分别在边AB和AC上,且DE∥BC.
如图,在△ABC中,点D,E分别在边AB和AC上,且DE∥BC.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y=(x+2)2-8 | B. | y=(x+2)2-4 | C. | y=(x+2)2+8 | D. | y=(x-2)2-8 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
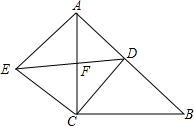 已知如图,△ABC是等腰三角形,∠ACB=90°,D是斜边AB上的一动点,联结CD,线段CD绕点C逆时针旋转90°,点D与点E重合,联结AE,DE,线段DE交边AC于点F.
已知如图,△ABC是等腰三角形,∠ACB=90°,D是斜边AB上的一动点,联结CD,线段CD绕点C逆时针旋转90°,点D与点E重合,联结AE,DE,线段DE交边AC于点F.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com