
ЁОЬтФПЁПвбжЊЕуAЃЌBЗжБ№ЪЧxжсЁЂyжсЩЯЕФЖЏЕуЃЌЕуCЃЌDЪЧФГИіКЏЪ§ЭМЯѓЩЯЕФЕуЃЌЕБЫФБпаЮABCDЃЈAЃЌBЃЌCЃЌDИїЕувРДЮХХСаЃЉЮЊе§ЗНаЮЪБЃЌЮвУЧГЦетИіе§ЗНаЮЮЊДЫКЏЪ§ЭМЯѓЕФЁААщТТе§ЗНаЮЁБЃЎ
Р§ШчЃКдкЭМ1жаЃЌе§ЗНаЮABCDЪЧвЛДЮКЏЪ§y=x+1ЭМЯѓЕФЦфжавЛИіЁААщТТе§ЗНаЮЁБЃЎ
ЃЈ1ЃЉШчЭМ1ЃЌШєФГКЏЪ§ЪЧвЛДЮКЏЪ§y=x+1ЃЌЧѓЫќЕФЭМЯѓЕФЫљгаЁААщТТе§ЗНаЮЁБЕФБпГЄЃЛ
ЃЈ2ЃЉШчЭМ2ЃЌШєФГКЏЪ§ЪЧЗДБШР§КЏЪ§ ![]() ЃЈkЃО0ЃЉЃЌЫќЕФЭМЯѓЕФЁААщТТе§ЗНаЮЁБЮЊABCDЃЌЕуDЃЈ2ЃЌmЃЉЃЈmЃМ2ЃЉдкЗДБШР§КЏЪ§ЭМЯѓЩЯЃЌЧѓmЕФжЕМАЗДБШР§КЏЪ§ЕФНтЮіЪНЃЛ
ЃЈkЃО0ЃЉЃЌЫќЕФЭМЯѓЕФЁААщТТе§ЗНаЮЁБЮЊABCDЃЌЕуDЃЈ2ЃЌmЃЉЃЈmЃМ2ЃЉдкЗДБШР§КЏЪ§ЭМЯѓЩЯЃЌЧѓmЕФжЕМАЗДБШР§КЏЪ§ЕФНтЮіЪНЃЛ
ЃЈ3ЃЉШчЭМ3ЃЌШєФГКЏЪ§ЪЧЖўДЮКЏЪ§y=ax2+cЃЈaЁй0ЃЉЃЌЫќЕФЭМЯѓЕФЁААщТТе§ЗНаЮЁБЮЊABCDЃЌCЃЌDжаЕФвЛИіЕузјБъЮЊЃЈ3ЃЌ4ЃЉЃЌЧыФужБНгаДГіИУЖўДЮКЏЪ§ЕФНтЮіЪНЃЎ
ЁОД№АИЁП
ЃЈ1ЃЉНтЃКЃЈIЃЉЕБЕуAдкxжсе§АыжсЁЂЕуBдкyжсИКАыжсЩЯЪБЃК
е§ЗНаЮABCDЕФБпГЄЮЊ ![]() ЃЎ
ЃЎ
ЃЈIIЃЉЕБЕуAдкxжсИКАыжсЁЂЕуBдкyжсе§АыжсЩЯЪБЃК
Щше§ЗНаЮБпГЄЮЊaЃЌвзЕУ3a= ![]() ЃЌ
ЃЌ
НтЕУa= ![]() ЃЌДЫЪБе§ЗНаЮЕФБпГЄЮЊ
ЃЌДЫЪБе§ЗНаЮЕФБпГЄЮЊ ![]() ЃЎ
ЃЎ
ЁрЫљЧѓЁААщТТе§ЗНаЮЁБЕФБпГЄЮЊ ![]() Лђ
Лђ ![]()
ЃЈ2ЃЉНтЃКШчЭМЃЌзїDEЁЭxжсЃЌCFЁЭyжсЃЌДЙзуЗжБ№ЮЊЕуEЁЂFЃЌ
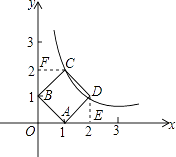
взжЄЁїADEЁеЁїBAOЁеЁїCBFЃЎ
ЁпЕуDЕФзјБъЮЊЃЈ2ЃЌmЃЉЃЌmЃМ2ЃЌ
ЁрDE=OA=BF=mЃЌ
ЁрOB=AE=CF=2ЉmЃЎ
ЁрOF=BF+OB=2ЃЌ
ЁрЕуCЕФзјБъЮЊЃЈ2ЉmЃЌ2ЃЉЃЎ
Ёр2m=2ЃЈ2ЉmЃЉЃЌНтЕУm=1ЃЎ
ЁрЗДБШР§КЏЪ§ЕФНтЮіЪНЮЊy= ![]()
ЃЈ3ЃЉНтЃКЪЕМЪЧщПіЪЧХзЮяЯпПЊПкЯђЩЯЕФСНжжЧщПіжаЃЌСэвЛИіЕуЖМдкЃЈ3ЃЌ4ЃЉЕФзѓВрЃЌЖјПЊПкЯђЯТЪБЃЌСэвЛЕуЖМдкЃЈ3ЃЌ4ЃЉЕФгвВрЃЌгыЩЯЪіНтЮіУїЯдВЛЗћКЯ
aЁЂЕБЕуAдкxжсе§АыжсЩЯЃЌЕуBдкyжсе§АыжсЩЯЃЌЕуCзјБъЮЊЃЈ3ЃЌ4ЃЉЪБЃКСэЭтвЛИіЖЅЕуЮЊЃЈ4ЃЌ1ЃЉЃЌЖдгІЕФКЏЪ§НтЮіЪНЪЧy=Љ ![]() x2+
x2+ ![]() ЃЛ
ЃЛ
bЁЂЕБЕуAдкx жсе§АыжсЩЯЃЌЕу Bдк yжсе§АыжсЩЯЃЌЕуD зјБъЮЊЃЈ3ЃЌ4ЃЉЪБЃКВЛДцдкЃЌ
cЁЂЕБЕуA дк x жсе§АыжсЩЯЃЌЕу Bдк yжсИКАыжсЩЯЃЌЕуC зјБъЮЊЃЈ3ЃЌ4ЃЉЪБЃКВЛДцдк
dЁЂЕБЕуAдкx жсе§АыжсЩЯЃЌЕуBдкyжсИКАыжсЩЯЃЌЕуDзјБъЮЊЃЈ3ЃЌ4ЃЉЪБЃКСэЭтвЛИіЖЅЕуCЮЊЃЈЉ1ЃЌ3ЃЉЃЌЖдгІЕФКЏЪ§ЕФНтЮіЪНЪЧy= ![]() x2+
x2+ ![]() ЃЛ
ЃЛ
eЁЂЕБЕуAдкxжсИКАыжсЩЯЃЌЕуBдкyжсИКАыжсЩЯЃЌЕуCзјБъЮЊЃЈ3ЃЌ4ЃЉЪБЃЌСэвЛИіЖЅЕуDЕФзјБъЪЧЃЈ7ЃЌЉ3ЃЉЪБЃЌЖдгІЕФКЏЪ§НтЮіЪНЪЧy=Љ ![]() x2+
x2+ ![]() ЃЛ
ЃЛ
fЁЂЕБЕуAдкxжсИКАыжсЩЯЃЌЕуBдкyжсИКАыжсЩЯЃЌЕуCзјБъЮЊЃЈ3ЃЌ4ЃЉЪБЃЌСэвЛИіЖЅЕуDЕФзјБъЪЧЃЈЉ4ЃЌ7ЃЉЪБЃЌЖдгІЕФХзЮяЯпЮЊy= ![]() x2+
x2+ ![]() ЃЛ
ЃЛ
ЙЪЖўДЮКЏЪ§ЕФНтЮіЪНЗжБ№ЮЊЃКy= ![]() x2+
x2+ ![]() Лђy=Љ
Лђy=Љ ![]() x2+
x2+ ![]() Лђy=Љ
Лђy=Љ ![]() x2+
x2+ ![]() Лђy=
Лђy= ![]() x2+
x2+ ![]()
ЁОНтЮіЁПЃЈ1ЃЉЯШе§ШЗЕиЛГіЭМаЮЃЌдйРћгУе§ЗНаЮЕФаджЪШЗЖЈЯрЙиЕуЕФзјБъДгЖјМЦЫуе§ЗНаЮЕФБпГЄ.
ЃЈ2ЃЉвђЮЊABCDЮЊе§ЗНаЮЃЌЫљвдПЩзїДЙЯпЕУЕНЕШбќжБНЧШ§НЧаЮЃЌРћгУЕуDЃЈ2ЃЌmЃЉЕФзјБъБэЪОГіЕуCЕФзјБъЃЌПЩЧѓГіmЕФжЕ ЃЌМДПЩЕУЕНЗДБШР§КЏЪ§ЕФНтЮіЪНЃЎ
ЃЈ3ЃЉгЩХзЮяЯпПЊПкМШПЩФмЯђЩЯЃЌвВПЩФмЯђЯТЃЎЕБХзЮяЯпПЊПкЯђЩЯЪБЃЌе§ЗНаЮЕФСэвЛИіЖЅЕувВЪЧдкХзЮяЯпЩЯЃЌетИіЕуМШПЩФмдкЕуЃЈ3ЃЌ4ЃЉЕФзѓБпЃЌвВПЩФмдкЕуЃЈ3ЃЌ4ЃЉЕФгвБпЃЌЙ§ЕуЃЈ3ЃЌ4ЃЉЯђxжсзїДЙЯпЃЌРћгУШЋЕШШ§НЧаЮШЗЖЈЯпЖЮЕФГЄМДПЩШЗЖЈХзЮяЯпЩЯСэвЛИіЕуЕФзјБъЃЛЕБХзЮяЯпПЊПкЯђЯТЪБвВЪЧвЛбљЕиЗжЮЊСНжжЧщПіРДЬжТлЃЌМДПЩЕУЕНЫљЧѓЕФНсТлЃЎ
ЁОПМЕуОЋЮіЁПЭЈЙ§СщЛюдЫгУЗДБШР§КЏЪ§ЕФЭМЯѓКЭЗДБШР§КЏЪ§ЕФаджЪЃЌеЦЮеЗДБШР§КЏЪ§ЕФЭМЯёЪєгкЫЋЧњЯпЃЎЗДБШР§КЏЪ§ЕФЭМЯѓМШЪЧжсЖдГЦЭМаЮгжЪЧжааФЖдГЦЭМаЮЃЎгаСНЬѕЖдГЦжсЃКжБЯпy=xКЭ y=-xЃЎЖдГЦжааФЪЧЃКдЕуЃЛаджЪ:ЕБkЃО0ЪБЫЋЧњЯпЕФСНжЇЗжБ№ЮЛгкЕквЛЁЂЕкШ§ЯѓЯоЃЌдкУПИіЯѓЯоФкyжЕЫцxжЕЕФдіДѓЖјМѕаЁЃЛ ЕБkЃМ0ЪБЫЋЧњЯпЕФСНжЇЗжБ№ЮЛгкЕкЖўЁЂЕкЫФЯѓЯоЃЌдкУПИіЯѓЯоФкyжЕЫцxжЕЕФдіДѓЖјдіДѓМДПЩвдНтД№ДЫЬтЃЎ


 дФЖСПьГЕЯЕСаД№АИ
дФЖСПьГЕЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
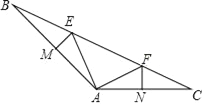
ЁОЬтФПЁПШчЭМЃЌвбжЊЁїABCжаЁЯBAC=135ЁуЃЌЕуEЃЌЕуFдкBCЩЯЃЌEMДЙжБЦНЗжABНЛABгкЕуMЃЌFNДЙжБЦНЗжACНЛACгкЕуNЃЌBE=12ЃЌCF=9ЃЎ
ЃЈ1ЃЉХаЖЯЁїEAFЕФаЮзДЃЌВЂЫЕУїРэгЩЃЛ
ЃЈ2ЃЉЧѓЁїEAFЕФжмГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
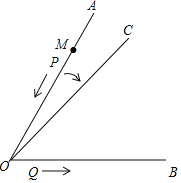
ЁОЬтФПЁПШчЭМЃЌвбжЊЁЯAOB=60ЁуЃЌЁЯAOBЕФБпOAЩЯгавЛЖЏЕуPЃЌДгОрРыOЕу18cmЕФЕуMДІГіЗЂЃЌбиЯпЖЮMOЁЂЩфЯпOBдЫЖЏЃЌЫйЖШЮЊ2cm/sЃЛЖЏЕуQДгЕуOГіЗЂЃЌбиЩфЯпOBдЫЖЏЃЌЫйЖШЮЊlcm/sЃЛPЁЂQЭЌЪБГіЗЂЃЌЭЌЪБЩфЯпOCШЦзХЕуOДгOAЩЯвдУПУы5ЁуЕФЫйЖШЫГЪБеыа§зЊЃЌЩшдЫЖЏЪБМфЪЧtЃЈsЃЉЃЎ
ЃЈ1ЃЉЕБЕуPдкMOЩЯдЫЖЏЪБЃЌPO=______cmЃЈгУКЌtЕФДњЪ§ЪНБэЪОЃЉЃЛ
ЃЈ2ЃЉЕБЕуPдкЯпЖЮMOЩЯдЫЖЏЪБЃЌtЮЊКЮжЕЪБЃЌOP=OQЃПДЫЪБЩфЯпOCЪЧЁЯAOBЕФНЧЦНЗжЯпТ№ЃПШчЙћЪЧЧыЫЕУїРэгЩЃЎ
ЃЈ3ЃЉдкЩфЯпOBЩЯЪЧЗёДцдкPЁЂQЯрОр2cmЃПШєДцдкЃЌЧыЧѓГіtЕФжЕВЂЧѓГіДЫЪБЁЯBOCЕФЖШЪ§ЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПГЫЗЈЙЋЪНЕФЬНОПМАгІгУЃЎ
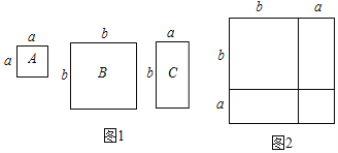
Ъ§бЇЛюЖЏПЮЩЯЃЌРЯЪІзМБИСЫШєИЩИіШчЭМ1ЕФШ§жжжНЦЌЃЌAжжжНЦЌБпГЄЮЊaЕФе§ЗНаЮЃЌBжжжНЦЌЪЧБпГЄЮЊbЕФе§ЗНаЮЃЌCжжжНЦЌГЄЮЊaЁЂПэЮЊbЕФГЄЗНаЮЃЌВЂгУAжжжНЦЌвЛеХЃЌBжжжНЦЌвЛеХЃЌCжжжНЦЌСНеХЦДГЩШчЭМ2ЕФДѓе§ЗНаЮЃЎ
(1)ЧыгУСНжжВЛЭЌЕФЗНЗЈЧѓЭМ2Дѓе§ЗНаЮЕФУцЛ§ЃЎЗНЗЈ1ЃК______ЃЛЗНЗЈ2ЃК_______ЃЎ
(2)ЙлВьЭМ2ЃЌЧыФуаДГіЯТСаШ§ИіДњЪ§ЪНЃК(a+b)2ЃЌa2+b2ЃЌabжЎМфЕФЕШСПЙиЯЕЃЎ_______ЃЛ
(3)РрЫЦЕФЃЌЧыФугУЭМ1жаЕФШ§жжжНЦЌЦДвЛИіЪЙГЄЗНаЮУцЛ§ЮЊЃК3a2+7ab+2b2ЃЌВЂЖд3a2+7ab+2b2вђЪНЗжНтЮЊ_______.
(4)ИљОн(2)ЬтжаЕФЕШСПЙиЯЕЃЌНтОіШчЯТЮЪЬтЃК
ЂйвбжЊЃКa+bЃН5ЃЌa2+b2ЃН11ЃЌЧѓabЕФжЕЃЛ
ЂквбжЊ(xЉ2016)2+(xЉ2018)2ЃН34ЃЌЧѓ(xЉ2017)2ЕФжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЫФБпаЮABCDжаЃЌЁЯA=90ЁуЃЌADЁЮBCЃЌEЮЊABЕФжаЕуЃЌСЌНгCEЃЌBDЃЌЙ§ЕуEзїFEЁЭCEгкЕуEЃЌНЛADгкЕуFЃЌСЌНгCFЃЌвбжЊ2AD=AB=BCЃЎ
ЃЈ1ЃЉЧѓжЄЃКCE=BDЃЛ
ЃЈ2ЃЉШєAB=4ЃЌЧѓAFЕФГЄЖШЃЛ
ЃЈ3ЃЉЧѓsinЁЯEFCЕФжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдке§ЗНаЮЭјИёжаЃЌУПИіаЁе§ЗНаЮЕФБпГЄОљЮЊ1ИіЕЅЮЛГЄЖШЃЌЁїABCЕФШ§ИіЖЅЕуЕФЮЛжУШчЭМЫљЪОЃЎЯжНЋЁїABCбизХЕуAЕНЕуDЕФЗНЯђЦНвЦЃЌЪЙЕуAБфЛЛЮЊЕуDЃЌЕуEЁЂFЗжБ№ЪЧBЁЂCЕФЖдгІЕуЃЎ
ЃЈ1ЃЉЛГіЁїABCжаABБпЩЯЕФИпCHЃЛЃЈЬсабЃКБ№ЭќСЫБъзЂзжФИЃЉЃЛ
ЃЈ2ЃЉЧыЛГіЦНвЦКѓЕФЁїDEFЃЛ
ЃЈ3ЃЉЦНвЦКѓЃЌЯпЖЮABЩЈЙ§ЕФВПЗжЫљзщГЩЕФЗтБеЭМаЮЕФУцЛ§ЪЧ___________.

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЙЋЫОгћеаЦИвЛУћВПУХОРэЃЌЖдМзЁЂввЁЂБћШ§УћКђбЁШЫНјааСЫШ§ЯюЫижЪВтЪдЃЎИїЯюВтЪдГЩМЈШчБэИёЫљЪОЃК
ВтЪдЯюФП | ВтЪдГЩМЈ | ||
Мз | вв | Бћ | |
зЈвЕжЊЪЖ | 74 | 87 | 90 |
гябдФмСІ | 58 | 74 | 70 |
злКЯЫижЪ | 87 | 43 | 50 |
ЃЈ1ЃЉШчЙћИљОнШ§ДЮВтЪдЕФЦНОљГЩМЈШЗЖЈШЫбЁЃЌФЧУДЫНЋБЛТМгУЃП
ЃЈ2ЃЉИљОнЪЕМЪашвЊЃЌЙЋЫОНЋзЈвЕжЊЪЖЁЂгябдФмСІКЭзлКЯЫижЪШ§ЯюВтЪдЕУЗжАД4ЃК3ЃК1ЕФБШР§ШЗЖЈУПИіШЫЕФВтЪдзмГЩМЈЃЌДЫЪБЫНЋБЛТМгУЃП
ЃЈ3ЃЉЧыжиаТЩшМЦзЈвЕжЊЪЖЁЂгябдФмСІКЭзлКЯЫижЪШ§ЯюВтЪдЕУЗжЕФБШР§РДШЗЖЈУПИіШЫЕФВтЪдзмГЩМЈЃЌЪЙЕУввБЛТМгУЃЌШєжиаТЩшМЦЕФБШР§ЮЊxЃКyЃК1ЃЌЧвx+y+1ЃН10ЃЌдђxЃНЁЁ ЁЁЃЌyЃНЁЁ ЁЁЃЎЃЈаДГіxгыyЕФвЛзщећЪ§жЕМДПЩЃЉЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЙЋЫОЮЊНБРјдкШЄЮЖдЫЖЏЛсЩЯШЁЕУКУГЩМЈЕФдБЙЄЃЌМЦЛЎЙКТђМзЁЂввСНжжНБЦЗЙВ20МўЃЎЦфжаМзжжНБЦЗУПМў40дЊЃЌввжжНБЦЗУПМў30дЊ
ЃЈ1ЃЉШчЙћЙКТђМзЁЂввСНжжНБЦЗЙВЛЈЗбСЫ650дЊЃЌЧѓМзЁЂввСНжжНБЦЗИїЙКТђСЫЖрЩйМўЃП
ЃЈ2ЃЉШчЙћЙКТђввжжНБЦЗЕФМўЪ§ВЛГЌЙ§МзжжНБЦЗМўЪ§ЕФ2БЖЃЌзмЛЈЗбВЛГЌЙ§680дЊЃЌЧѓИУЙЋЫОгаФФМИжжВЛЭЌЕФЙКТђЗНАИЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПгУОиаЮжНЦЌелГіжБНЧЕФЦНЗжЯпЃЌЯТСаелЗЈе§ШЗЕФЪЧЃЈ ЃЉ
A.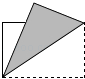
B.
C.
D.
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com