
【题目】乘法公式的探究及应用.
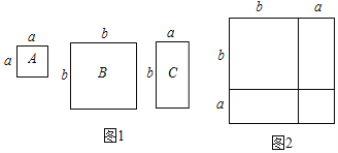
数学活动课上,老师准备了若干个如图1的三种纸片,A种纸片边长为a的正方形,B种纸片是边长为b的正方形,C种纸片长为a、宽为b的长方形,并用A种纸片一张,B种纸片一张,C种纸片两张拼成如图2的大正方形.
(1)请用两种不同的方法求图2大正方形的面积.方法1:______;方法2:_______.
(2)观察图2,请你写出下列三个代数式:(a+b)2,a2+b2,ab之间的等量关系._______;
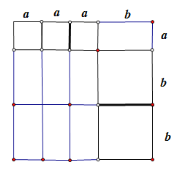
(3)类似的,请你用图1中的三种纸片拼一个使长方形面积为:3a2+7ab+2b2,并对3a2+7ab+2b2因式分解为_______.
(4)根据(2)题中的等量关系,解决如下问题:
①已知:a+b=5,a2+b2=11,求ab的值;
②已知(x﹣2016)2+(x﹣2018)2=34,求(x﹣2017)2的值.
【答案】(1)(a+b)2;a2+b2+2ab;(2)(a+b)2=a2+2ab+b2;(3)3a2+7ab+2b2=(a+2b)(3a+b);(4)①ab=7;②(x﹣2017)2=16.
【解析】
(1)直接利用大正方形的边长×边长;将所有的小正方形与矩形的面积相加;
(2)根据(1)与大正方形的面积不变即可得解;
(3)根据题意画出图形,再利用面积相等的列出等式即可;
(4)①根据题意将a+b平方,利用完全平方公式变形求解即可;
②利用完全平方公式去括号将原式变为2(x2﹣2×2017x+20172)+20182+20162﹣2×20172=34,再利用平方差公式变形求解即可.
解:(1)大正方形的边长为a+b,则其面积为(a+b)2;
两个小正方形的面积为a2,b2,长方形的面积为2ab,则其面积为a2+b2+2ab;
(2)根据大正方形的面积相等得:(a+b)2=a2+2ab+b2;
(3)如图,可得3a2+7ab+2b2=(a+2b)(3a+b);
(4)①(a+b)2= a2+2ab+b2=25,
∵a2+b2=11,
∴2ab=14,
解得ab=7;
②∵(x﹣2016)2+(x﹣2018)2=34,
∴x2﹣2×2016x+20162+x2﹣2×2018x+20182=34,
∴2(x2﹣2×2017x+20172)+20182+20162﹣2×20172=34,
∴2(x﹣2017)2+2018+2017﹣2016﹣2017=34,
则(x﹣2017)2=16.


 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,直线l1∥l2,以直线l1上的点A为圆心,适当长为半径画弧,分别交直线l1和l2于B、C两点,连接AC、BC,若∠ABC=65°,则∠1的度数是( )

A. 35° B. 50° C. 65° D. 70°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题情境:如图1,AB∥CD,∠PAB=130°,∠PCD=120°,求∠APC的度数.
小明的思路是:过P作PE∥AB,通过平行线性质来求∠APC.
(1)按小明的思路,易求得∠APC的度数为_____度;
(2)问题迁移:如图2,AB∥CD,点P在射线OM上运动,记∠PAB=α,∠PCD=β,当点P在B、D两点之间运动时,问∠APC与α、β之间有何数量关系?请说明理由;
(3)在(2)的条件下,如果点P在B、D两点外侧运动时(点P与点O、B、D三点不重合),请直接写出∠APC与α、β之间的数量关系.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,以BC为直径的⊙O交AB于点D,E是AC的中点,OE交CD于点F.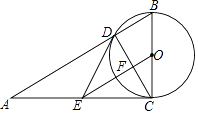
(1)若∠BCD=36°,BC=10,求BD的长;
(2)判断直线DE与⊙O的位置关系,并说明理由;
(3)求证:2CE2=ABEF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点A,B分别是x轴、y轴上的动点,点C,D是某个函数图象上的点,当四边形ABCD(A,B,C,D各点依次排列)为正方形时,我们称这个正方形为此函数图象的“伴侣正方形”.
例如:在图1中,正方形ABCD是一次函数y=x+1图象的其中一个“伴侣正方形”.
(1)如图1,若某函数是一次函数y=x+1,求它的图象的所有“伴侣正方形”的边长;
(2)如图2,若某函数是反比例函数 ![]() (k>0),它的图象的“伴侣正方形”为ABCD,点D(2,m)(m<2)在反比例函数图象上,求m的值及反比例函数的解析式;
(k>0),它的图象的“伴侣正方形”为ABCD,点D(2,m)(m<2)在反比例函数图象上,求m的值及反比例函数的解析式;
(3)如图3,若某函数是二次函数y=ax2+c(a≠0),它的图象的“伴侣正方形”为ABCD,C,D中的一个点坐标为(3,4),请你直接写出该二次函数的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】感知:
如图①,AD平分∠BAC,∠B+∠C=180°,∠B=90°.判断DB与DC的大小关系并证明.
探究:
如图②,AD平分∠BAC,∠ABD+∠ACD=180°,∠ABD<90°,DB与DC的大小关系变吗?请说明理由.
应用:
如图③,四边形ABDC中,∠B=45°,∠C=135°,DB=DC=a,则AB﹣AC= .(用含a的代数式表示)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,现有5张写着不同数字的卡片,请按要求完成下列问题:
![]()
![]() 若从中取出2张卡片,使这2张卡片上数字的乘积最大,则乘积的最大值是______.
若从中取出2张卡片,使这2张卡片上数字的乘积最大,则乘积的最大值是______.
![]() 若从中取出2张卡片,使这2张卡片上数字相除的商最小,则商的最小值是______.
若从中取出2张卡片,使这2张卡片上数字相除的商最小,则商的最小值是______.
![]() 若从中取出4张卡片,请运用所学的计算方法,写出两个不同的运算式,使四个数字的计算结果为24.
若从中取出4张卡片,请运用所学的计算方法,写出两个不同的运算式,使四个数字的计算结果为24.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com