
【题目】巴蜀中学2017春季运动会的开幕式精彩纷呈,主要分为以下几个类型:A文艺范、B动漫潮、C学院派、D民族风,为了解未能参加运动会的初三学子对开幕式类型的喜好情况,学生处在初三年级随机抽取了一部分学生进行调查,并将他们喜欢的种类绘制成如下统计图,请你根据统计图解答以下问题: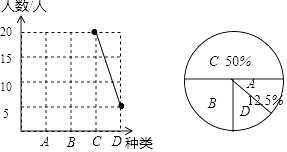
(1)请补全折线统计图,并求出“动漫潮”所在扇形的圆心角度数.
(2)据统计,在被调查的学生中,喜欢“文艺范”类型的仅有2名住读生,其余均为走读生,初二年级欲从喜欢“文艺范”的这几名同学中随机抽取两名同学去观摩“文明礼仪大赛”视频,用列表法或树状图的方法求出所选的两名同学都是走读生的概率.
【答案】
(1)解:被调查的学生数为;20÷50%=40人,
A文艺范人数=40×12.5%=5人,
B动漫潮人数=40﹣5﹣5﹣20=10人,
补全折线统计图如图所示,
“动漫潮”所在扇形的圆心角度数=360°× ![]() =90°
=90°

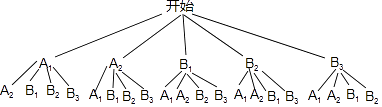
(2)解:设2名住读生为A1,A2,走读生为B1,B2,B3画树状图如图所示,
有树状图得知,所有等可能的情况有20种,其中所选两位同学恰好都是都是走读生的情况有6种,
∴所选的两名同学都是走读生的概率= ![]() =
= ![]() .
.
【解析】(1)根据等级C的人数除以占的百分比求出调查的学生数,进而确定出等级A的人数即可,补全条形统计图即可;
(2)设2名住读生为A1,A2,走读生为B1,B2,B3画树状图如图所示,有树状图得知,所有等可能的情况有20种,其中所选两位同学恰好都是都是走读生的情况有6种,根据概率公式计算即可。
【考点精析】本题主要考查了扇形统计图和折线统计图的相关知识点,需要掌握能清楚地表示出各部分在总体中所占的百分比.但是不能清楚地表示出每个项目的具体数目以及事物的变化情况;能清楚地反映事物的变化情况,但是不能清楚地表示出在总体中所占的百分比才能正确解答此题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
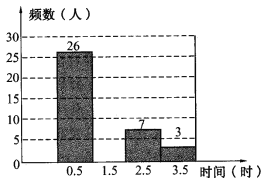
【题目】为了解某城镇中学学做家务的时间,一综合实践活动小组对该班50名学生进行了调查,根据调查所得的数据制成如下图的频数分布直方图.
(1)补全该图,并写出相应的频数;
(2)求第1组的频率;
(3)求该班学生每周做家务时间的平均数;
(4)你的做家务时间在哪一组内?请用一句话谈谈你的感受.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图a、图b是两张形状、大小完全相同的方格纸,方格纸中每个小正方形的边长均为1,点A、B在小正方形的顶点上.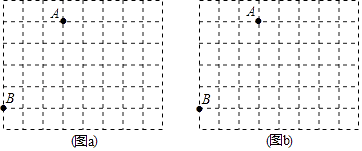
(1)在图a中画出△ABC(点C在小正方形的顶点上),使△ABC是等腰三角形且△ABC为钝角三角形;
(2)在图b中画出△ABD(点D在小正方形的顶点上),使△ABD是等腰三角形,且tan∠ABD=1.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中, △ABC如图(每个小正方形的边长均为1).

(1)请画出△ABC沿x轴向右平移4个单位长度,再沿y轴向上平移2个单位长度后的△A′B′C′(其中A′、B′、C′分别是A、B、C的对应点,不写画法)
(2)直接写出A′、B′、C′三点的坐标:A′(____,_____); B′(____,_____);C′(____,_____).
(3)求△A′B′C′的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司员工的月工资如下表:
员工 | 经理 | 副经理 | 职员A | 职员B | 职员C | 职员D | 职员E | 职员F | 职员G |
月工资/元 | 4800 | 3500 | 2000 | 1900 | 1800 | 1600 | 1600 | 1600 | 1000 |
则这组数据的平均数、众数、中位数分别为( )
A. 2200元 1800元 1600元 B. 2000元 1600元 1800元
C. 2200元 1600元 1800元 D. 1600元 1800元 1900元
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某制衣厂某车间计划用10天加工一批出口童装和成人装共360件,该车间的加工能力是:每天能单独加工童装45件或成人装30件。
(1)该车间应安排几天加工童装,几天加工成人装,才能如期完成任务?
(2)若加工童装一件可获利80元, 加工成人装一件可获利120元, 那么该车间加工完这批服装后,共可获利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是平行四边形,下列说法不正确的是( )
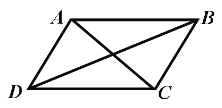
A. 当AC=BD时,四边形ABCD是矩形
B. 当AB=BC时,四边形ABCD是菱形
C. 当AC⊥BD时,四边形ABCD是菱形
D. 当∠DAB=90°时,四边形ABCD是正方形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】完成下面的证明.
已知,如图所示,BCE,AFE是直线,
AB∥CD,∠1=∠2,∠3=∠4.
求证:AD∥BE
证明:∵ AB∥CD (已知)
∴ ∠4 =∠ ( )
∵ ∠3 =∠4 (已知)
∴ ∠3 =∠ ( )
∵∠1 =∠2 (已知)
∴∠1+∠CAF =∠2+ ∠CAF ( )
即:∠ =∠ .
∴ ∠3 =∠ ( )
∴ AD∥BE ( )

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com