
����Ŀ����֪������y=ax2+bx+3��y��Ľ���ΪA����A���B���������ߵĶԳ���Գƣ����κ���y=ax2+bx+3��y��x�IJ��ֶ�Ӧֵ���±���
x | �� | ��1 | 0 | 1 | 3 | 4 | �� |
y | �� | 8 | 0 | 0 | �� |
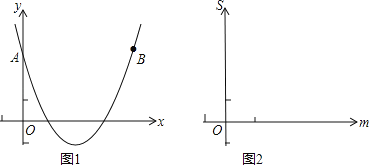
��1�������ߵĶԳ����� _________ ����A�� ______�� ____����B�� _____�� _____����
��2������κ���y=ax2+bx+3�Ľ���ʽ��
��3����֪��M��m��n����������y=ax2+bx+3�ϣ����BAM�����ΪS����S��m�ĺ�����ϵʽ����������ͼ�����ú���ͼ��˵��S�Ƿ�������ֵ��Ϊʲô��
���𰸡���1��x=2��A��0��3����B��4��3����
��2��y=x2-4x+3��
��3��S=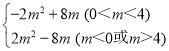 ��S���������ֵ����ͼ���֪����m��0��m��4ʱ��S��ֵ��������
��S���������ֵ����ͼ���֪����m��0��m��4ʱ��S��ֵ��������
��������
������1�����õ�x=1��3ʱ��y=0���ó������ߵĶԳ�����ֱ��x=2��������x=0ʱ��y=3�����A�� 0��3 �������ɵó�B�����ꣻ
��2������ͼ�����1��0������3��0������������Ϊy=a��x-1����x-3��������0��3������ɵó�a��ֵ�������ó�����ʽ��
��3����0��m��4ʱ����M��AB�ľ���Ϊ3-n����m��0��m��4ʱ����M��ֱ��AB�ľ���Ϊn-3����������������ó�S��m�ĺ�����ϵʽ������ͼ��ó�S�Ƿ�������ֵ��
�����������1�����ݵ�x=1��3ʱ��y=0���ó������ߵĶԳ����ǣ�ֱ��x=2��
��������y=ax2+bx+3��y��Ľ���ΪA��
��x=0ʱ��y=3�����A��0��3������B��4��3����
��2��ͼ�����1��0������3��0����
��������Ϊy=a��x-1����x-3����
����0��3������ɵã�3=a��0-1����0-3����
��ã�a=1��
�ʶ��κ���y=ax2+bx+3�Ľ���ʽΪ��y=��x-1����x-3��=x2-4x+3��
��3����ͼ1��
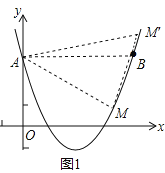
��AB��x�ᣬAB=4��
��0��m��4ʱ����M��AB�ľ���Ϊ3-n��
��S��ABM=![]() ��3-n����4=6-2n��
��3-n����4=6-2n��
����n=m2-4m+3��S1=-2m2+8m��
����m��0��m��4ʱ����M��ֱ��AB�ľ���Ϊn-3��S2=![]() ��4��n-3��=2n-6��
��4��n-3��=2n-6��
��n=m2-4m+3��S2=2m2-8m��
S=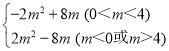 ��
��
�ʺ���ͼ����ͼ2��x���Ϸ���������ʾ��S���������ֵ����ͼ���֪����m��0��m��4ʱ��S��ֵ��������




| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
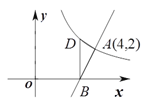
����Ŀ����ͼ��ֱ��![]() �뷴��������
�뷴��������![]() ��ͼ���ڵ�
��ͼ���ڵ�![]() ����
����![]() �ύ�ڵ�
�ύ�ڵ�![]() .
.
��1����![]() ��ֵ����
��ֵ����![]() �����ꣻ
�����ꣻ
��2������![]() ��
��![]()
![]() �ύ������������ͼ���ڵ�
�ύ������������ͼ���ڵ�![]() �����D�������
�����D�������![]() �������
�������
��3���۲�ͼ��д����x��0ʱ����ʽ![]() �Ľ⼯.
�Ľ⼯.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У�AB��AC����ABΪֱ���ġ�O�ֱ���BC��AC���ڵ�D��E������D��DF��AC������ΪF��
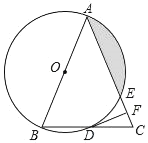
��1����֤��DFΪ��O�����ߣ�
��2����![]() ����CDF��22.5�㣬����Ӱ���ֵ������
����CDF��22.5�㣬����Ӱ���ֵ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С���о�һ���������ʣ��±��Ǹú����ļ����Ӧֵ��

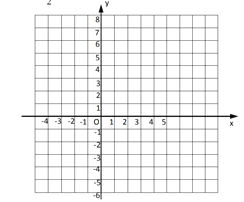
![]() ��ƽ��ֱ������ϵ�У�������ϱ����еĸ��㣬��������ĵ㣬�����ú���ͼ��
��ƽ��ֱ������ϵ�У�������ϱ����еĸ��㣬��������ĵ㣬�����ú���ͼ��
![]() ������������ͼ��д���ú�����һ�����ʣ� .
������������ͼ��д���ú�����һ�����ʣ� .
![]() ����ͼ��ֱ��д���ú����Ľ���ʽ���Ա�����ȡֵ��Χ�� ��
����ͼ��ֱ��д���ú����Ľ���ʽ���Ա�����ȡֵ��Χ�� ��
![]() ��һ�κ���
��һ�κ���![]() ��ú���ͼ�����������㣬��
��ú���ͼ�����������㣬��![]() �ķ�Χ�� .
�ķ�Χ�� .
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪�ڡ�ABC�У�AB=AC�� ��1������A=36���ڡ�ABC�л�һ���߶Σ��ܵõ�2�����������Σ���������ABC������2�����������εĶ��ǵĶ����ֱ���_____����2������A��36�� ����A=_____ʱ���ڵ�����ABC�л�һ���߶Σ��ܵõ�2�����������Σ���������ABC��.��д�������𰸼��ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����![]() ������Ϊ
������Ϊ![]() ������
������![]() �ӵ�
�ӵ�![]() ��������
��������![]() ����ÿ��
����ÿ��![]() ����λ���ٶ������ƶ����ҹ���
����λ���ٶ������ƶ����ҹ���![]() ��ֱ��
��ֱ��![]() Ҳ��֮�ƶ��������
Ҳ��֮�ƶ��������![]() ����
����![]() �ĶԳƵ������������ϣ�û��
�ĶԳƵ������������ϣ�û��![]() ���ƶ�ʱ��Ϊ
���ƶ�ʱ��Ϊ![]() ����ô
����ô![]() ��ֵ������___.
��ֵ������___.
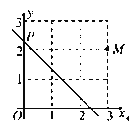
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
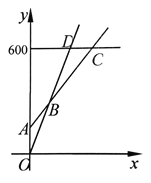
����Ŀ��ijƹ�������ͨƱ��20Ԫ/�ţ����Ϊ�˴��������Ƴ������Żݿ����ٽ��ۼ�600Ԫ/�ţ�ÿ��ƾ�������շѣ��������ۼ�150Ԫ/�ţ�ÿ��ƾ������10Ԫ��������ͨƱ�������ۣ������Żݿ���������ʹ�ã������������ƹ��x��ʱ�������ܷ���ΪyԪ��
��1���ֱ�д��ѡ����������ͨƱ����ʱ��y��x֮��ĺ�����ϵʽ��
��2����ͬһ������ϵ�У����������ѷ�ʽ��Ӧ�ĺ���ͼ����ͼ��ʾ������ݺ���ͼ��д��ѡ���������ѷ�ʽ������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ����ϣ�����̵Ľⷨ
���һԪһ�η��̣����ݵ�ʽ�Ļ������ʣ��ѷ���ת��Ϊx=a����ʽ������Ԫһ�η����飬����ת��ΪһԪһ�η������⣻���Ƶģ������Ԫһ�η����飬����ת��Ϊ���Ԫһ�η����飮���һԪ���η��̣�����ת��Ϊ����һԪһ�η������⣮����ʽ���̣�����ת��Ϊ��ʽ�������⣬������ȥ��ĸ�����ܲ������������Խ��ʽ���̱�����飮����̵Ľⷨ������ͬ������������һ����ͬ�Ļ�����ѧ˼��![]() ת������δ֪ת��Ϊ��֪��
ת������δ֪ת��Ϊ��֪��
����ת��������ѧ˼�룬���ǻ����Խ�һЩ�µķ��̣����磬һԪ���η���x3+x2-2x=0������ͨ����ʽ�ֽ����ת��Ϊx(x2+x-2)=0���ⷽ��x=0��x2+x-2=0���ɵ÷���x3+x2-2x=0�Ľ⣮
��1�����⣺����x3+x2-2x=0�Ľ���x1=0,x2= ��x3= ��
��2����չ������ת����˼����![]() �Ľ⣻
�Ľ⣻
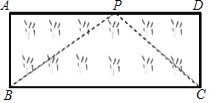
��3��Ӧ�ã���ͼ����֪���β�ƺABCD�ij�AD=8m����AB=3m��С����һ����Ϊ10m�����ӵ�һ�˹̶��ڵ�B���ز�ƺ����BA��AD�ߵ���P�����ѳ���PB����ֱ���̶��ڵ�P��Ȼ���ز�ƺ����PD��DC�ߵ���C�����ѳ���ʣ�µ�һ����ֱ����������һ��ǡ�����ڵ�C����AP�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˽���������ѧ�������Ķ����������С���������ѧ�ڳ���ѧ���Ķ������鼮�IJ��������˳������飬�����ݵ��������Ƴ�����ͳ��ͼ��
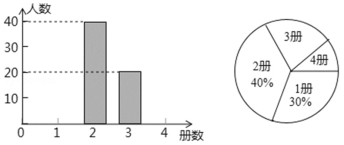
����ͳ��ͼ�ṩ����Ϣ������������⣺
��1������������������������ ����
��2����ȫ����ͳ��ͼ��
��3����������18000����������������������ѧ����ѧ�ڿ����Ķ�����2���������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com