
����Ŀ���Ķ����ϣ�����̵Ľⷨ
���һԪһ�η��̣����ݵ�ʽ�Ļ������ʣ��ѷ���ת��Ϊx=a����ʽ������Ԫһ�η����飬����ת��ΪһԪһ�η������⣻���Ƶģ������Ԫһ�η����飬����ת��Ϊ���Ԫһ�η����飮���һԪ���η��̣�����ת��Ϊ����һԪһ�η������⣮����ʽ���̣�����ת��Ϊ��ʽ�������⣬������ȥ��ĸ�����ܲ������������Խ��ʽ���̱�����飮����̵Ľⷨ������ͬ������������һ����ͬ�Ļ�����ѧ˼��![]() ת������δ֪ת��Ϊ��֪��
ת������δ֪ת��Ϊ��֪��
����ת��������ѧ˼�룬���ǻ����Խ�һЩ�µķ��̣����磬һԪ���η���x3+x2-2x=0������ͨ����ʽ�ֽ����ת��Ϊx(x2+x-2)=0���ⷽ��x=0��x2+x-2=0���ɵ÷���x3+x2-2x=0�Ľ⣮
��1�����⣺����x3+x2-2x=0�Ľ���x1=0,x2= ��x3= ��
��2����չ������ת����˼����![]() �Ľ⣻
�Ľ⣻
��3��Ӧ�ã���ͼ����֪���β�ƺABCD�ij�AD=8m����AB=3m��С����һ����Ϊ10m�����ӵ�һ�˹̶��ڵ�B���ز�ƺ����BA��AD�ߵ���P�����ѳ���PB����ֱ���̶��ڵ�P��Ȼ���ز�ƺ����PD��DC�ߵ���C�����ѳ���ʣ�µ�һ����ֱ����������һ��ǡ�����ڵ�C����AP�ij���
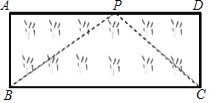
���𰸡�(1)-2��1����2��x=3����3��4m.
��������
��1����ʽ�ֽ����ʽ��Ȼ��ý��ۣ�
��2������ƽ��������������ת��Ϊ��ʽ���̣���⣬ע�������
��3����AP�ij�Ϊxm�����ݹ��ɶ�����BP+CP=10�����г����̣����ڷ��̺��и��ţ�����ƽ��������������ת��Ϊ��ʽ���̣���⣬
�⣺��1��![]() ��
��
![]() ��
��
![]()
����![]() ��
��![]() ��
��![]()
![]() ��
��![]() ��
��![]() ��
��
�ʴ�Ϊ��![]() ��1��
��1��
��2��![]() ��
��
���̵�����ƽ������![]()
��![]()
![]()
![]() ��
��![]()
![]() ��
��![]() ��
��
��![]() ʱ��
ʱ��![]() ��
��
����![]() ����ԭ���̵Ľ⣮
����ԭ���̵Ľ⣮
���Է���![]() �Ľ���
�Ľ���![]() ��
��
��3����Ϊ�ı���![]() �Ǿ��Σ�
�Ǿ��Σ�
����![]() ��
��![]()
��![]() ����
����![]()
��Ϊ![]() ��
��
![]() ��
��![]()
![]()
![]()
![]()
![]()
����ƽ������![]()
��������![]()
����ƽ������������![]()
��![]()
����![]() ��
��
�����飬![]() �Ƿ��̵Ľ⣮
�Ƿ��̵Ľ⣮
��![]() �ij�Ϊ
�ij�Ϊ![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
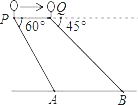
����Ŀ����ͼ��һ�������ھ����90�ߵ�P�����۲�����ϵ�A�ĸ���Ϊ60�㣬������ÿ��9���ٶ���AB�����ƶ���5�뵽��Q������ʱ�۲�����ϵ�B�ĸ���Ϊ45��.����P��Q��A��B��ͬһǦֱ���ϣ�.
(1)�������Q��������ǰ�ƶ������䣬�ٹ�����λ��B�����Ϸ���
(2)��AB�ij�������������ţ�.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
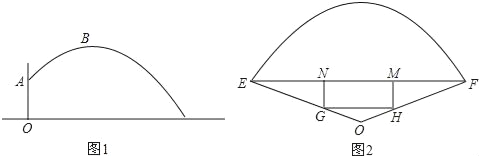
����Ŀ��ij����һ������OEF��ƺ�ϵ�Բ��O����ֱ�ڲ�ƺ�ĵ�����һ������OA����A����װһ���Զ���ˮװ�ã���ͷ������ˮ������ͷ���ڣ�����![]() m��ˮ���ڸ�������������״��ͬ��������·�����£������ˮ������D���ˮƽ����4�״��ﵽ��ߵ�B����B�������2�ף�����ͷA��ת120��ʱ�������ƺ����ȫ��ˮ���ǣ���ͼ1��ʾ��
m��ˮ���ڸ�������������״��ͬ��������·�����£������ˮ������D���ˮƽ����4�״��ﵽ��ߵ�B����B�������2�ף�����ͷA��ת120��ʱ�������ƺ����ȫ��ˮ���ǣ���ͼ1��ʾ��
��1�������ʵ�������ϵ��ʹA�������Ϊ��O��![]() ����ˮ������ߵ�B������Ϊ��4��2�������������ϵ��������ˮ����Ӧ�ĺ�����ϵʽ��
����ˮ������ߵ�B������Ϊ��4��2�������������ϵ��������ˮ����Ӧ�ĺ�����ϵʽ��
��2������ˮװ�������IJ�ƺ����������������ʾ����
��3��������OEF��һ������������ؿ��OEF�У���Ҫ����һ������GHMN��̳����ͼ2����Ʒ�����ʹH��G�ֱ���OF��OE�ϣ�MN��EF�ϣ���MN��2x����xȡ��ֵʱ������GHMN��̳���������������Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��y��x+c��x�ύ�ڵ�A����4��0������y�ύ�ڵ�C��������y����x2+bx+c������A��C��
��1���������ߵĽ���ʽ��
��2����֪��P���������ϵ�һ�����㣬���ҵ�P�ڵڶ������ڣ�������P��PE��x���ڵ�E�����߶�AC�ڵ�D��
����ͼ1����D��DF��y���ڵ�F������������M��N���㣨��Mλ�ڵ�N����ࣩ������EF�����߶�EF�ij������ʱ�����P��M��N�����ꣻ
����ͼ2������CD������C��P��DΪ��������������ADE���ƣ����CPD�������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�̳���ÿ��42Ԫ�ļ۸�һ�ַ�װ,������֪,ÿ�������t��ÿ�������ۼ�x(Ԫ��֮��ĺ�����ϵΪt=204-3x��
��1����д��ÿ���������ַ�װ��ë����y(Ԫ����ÿ�����ۼ�x(Ԫ��֮��ĺ�������ʽ��ë����=���ۼ�-�����ۣ��� ������Ա�����ȡֵ��Χ��
��2��ÿ�����ۼ�Ϊ����Ԫ������ʹÿ���ë����������ë�����Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
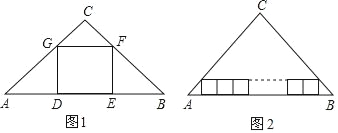
����Ŀ������ABC�У���C��90����AC��4��BC��3����ͼ1���ı���DEFGΪ��ABC���ڽ������Σ���������DEFG�ı߳�Ϊ_____����ͼ2����������ABC���в��ŵ�n��ȫ�ȵ������Σ�������ɵľ����ڽ�����ABC���������εı߳�Ϊ_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����3����ȫ��ͬ��С�����Ƿֱ���Ϊ1��2��3������һ���ڴ��У����������һ��С�Żأ������������һ��С��
(1) ��������ͼ��(���б���)�г�����������ֵ����п��ܽ����
(2) �����������������֮�͵���5�ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
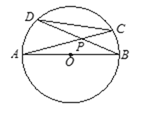
����Ŀ����ͼ����O��ֱ��AB=10��CD�ǡ�O���ң�AC��BD�ཻ�ڵ�P��
��1�����BPC=�������sin���Ƿ���5x2-13x��6=0�ĸ�����cos����ֵ��
��2���ڣ�1���������£�����CD�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������������y����![]() ��ͼ�����ͼ��ش�(1)��x��2ʱ��y��ֵ��(2)��1��x��4ʱ��y��ȡֵ��Χ��(3)��1��y��4ʱ��x��ȡֵ��Χ��
��ͼ�����ͼ��ش�(1)��x��2ʱ��y��ֵ��(2)��1��x��4ʱ��y��ȡֵ��Χ��(3)��1��y��4ʱ��x��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com