
【题目】如图,一热气球在距地面90米高的P处,观测地面上点A的俯角为60°,气球以每秒9米的速度沿AB方向移动,5秒到达Q处,此时观测地面上点B的俯角为45°.(点P,Q,A,B在同一铅直面上).
(1)若气球从Q处继续向前移动,方向不变,再过几秒位于B点正上方?
(2)求AB的长(结果保留根号).
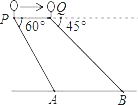
【答案】(1)10秒,(2)(135﹣30![]() )m.
)m.
【解析】
(1)首先过点B作BH⊥PQ,垂足为H,即可得出QH=HB=90m,进而利用平移速度得出答案;
(2)首先过点P作PE⊥AB,垂足为E,利用tan60°=![]() =
=![]() ,进而得出AE的长,再利用PH=BE进而得出AB的长.
,进而得出AE的长,再利用PH=BE进而得出AB的长.
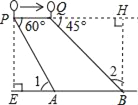
解:(1)过点B作BH⊥PQ,垂足为H,
∵一热气球在距地面90米高的P处,
∴HB=90m,
∵∠HQB=45°,
∴∠2=45°,
∴QH=HB=90m,
∴90÷9=10(秒),
答:气球从Q处继续向前移动,方向不变,再过10秒位于B点正上方;
(2)过点P作PE⊥AB,垂足为E,
∵一热气球在距地面90米高的P处,
∴PE=90m,
∵∠QPA=60°,
∴∠1=60°,
∴tan60°=![]() =
=![]() ,
,
∴AE=![]() =30
=30![]() ,
,
∵气球以每秒9米的速度沿AB方向移动,5秒到达Q处,
∴PQ=5×9=45(m),
∴PH=45+90=135(m),
∴BE=135(m),
∴AB=BE﹣AE=(135﹣30![]() )m,
)m,
答:AB的长为(135﹣30![]() )m.
)m.


科目:初中数学 来源: 题型:
【题目】如果把函数y=x2(x≤2)的图象和函数y=![]() 的图象组成一个图象,并称作图象E,那么直线y=3与图象E的交点有_____个;若直线y=m(m为常数)与图象E有三个不同的交点,则常数m的取值范围是_____.
的图象组成一个图象,并称作图象E,那么直线y=3与图象E的交点有_____个;若直线y=m(m为常数)与图象E有三个不同的交点,则常数m的取值范围是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于反比例函数y=![]() (k≠0),下列所给的四个结论中,正确的是( )
(k≠0),下列所给的四个结论中,正确的是( )
A. 若点(2,4)在其图象上,则(﹣2,4)也在其图象上
B. 当k>0时,y随x的增大而减小
C. 过图象上任一点P作x轴、y轴的垂线,垂足分别A、B,则矩形OAPB的面积为k
D. 反比例函数的图象关于直线y=x和y=﹣x成轴对称
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,反比例函数的图象经过点A、P,点A(6,![]() ),点P的横坐标是2.抛物线y=ax2+bx+c(a≠0)经过坐标原点,且与x轴交于点B,顶点为P.
),点P的横坐标是2.抛物线y=ax2+bx+c(a≠0)经过坐标原点,且与x轴交于点B,顶点为P.
求:(1)反比例函数的解析式;
(2)抛物线的表达式及B点坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】天塔是天津市的标志性建筑之一,某校数学兴趣小组要测量天塔的高度,如图,他们在点A处测得天塔最高点C的仰角为45°,再往天塔方向前进至点B处测得最高点C的仰角为54°,AB=112m,根据这个兴趣小组测得的数据,计算天塔的高度CD(tan36°≈0.73,结果保留整数).

查看答案和解析>>
科目:初中数学 来源: 题型:
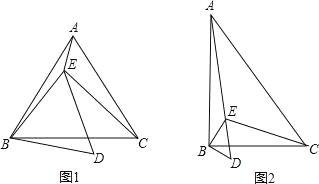
【题目】已知点E在△ABC内,∠ABC=∠EBD=α,∠ACB=∠EDB=60°,∠AEB=150°,∠BEC=90°.
(1)当α=60°时(如图1),
①判断△ABC的形状,并说明理由;
②求证:BD=![]() AE;
AE;
(2)当α=90°时(如图2),求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将函数y=![]() (x-2)2+1的图象沿y轴向上平移得到一条新函数的图象,其中点A(1,m),B(4,n)平移后的对应点分别为点A′,B′,若曲线段AB扫过的面积为9(图中的阴影部分),则新图象的函数表达式是__________.
(x-2)2+1的图象沿y轴向上平移得到一条新函数的图象,其中点A(1,m),B(4,n)平移后的对应点分别为点A′,B′,若曲线段AB扫过的面积为9(图中的阴影部分),则新图象的函数表达式是__________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:各类方程的解法
求解一元一次方程,根据等式的基本性质,把方程转化为x=a的形式.求解二元一次方程组,把它转化为一元一次方程来解;类似的,求解三元一次方程组,把它转化为解二元一次方程组.求解一元二次方程,把它转化为两个一元一次方程来解.求解分式方程,把它转化为整式方程来解,由于“去分母”可能产生增根,所以解分式方程必须检验.各类方程的解法不尽相同,但是它们有一个共同的基本数学思想![]() 转化,把未知转化为已知.
转化,把未知转化为已知.
用“转化”的数学思想,我们还可以解一些新的方程.例如,一元三次方程x3+x2-2x=0,可以通过因式分解把它转化为x(x2+x-2)=0,解方程x=0和x2+x-2=0,可得方程x3+x2-2x=0的解.
(1)问题:方程x3+x2-2x=0的解是x1=0,x2= ,x3= ;
(2)拓展:用“转化”思想求方程![]() 的解;
的解;
(3)应用:如图,已知矩形草坪ABCD的长AD=8m,宽AB=3m,小华把一根长为10m的绳子的一端固定在点B,沿草坪边沿BA,AD走到点P处,把长绳PB段拉直并固定在点P,然后沿草坪边沿PD、DC走到点C处,把长绳剩下的一段拉直,长绳的另一端恰好落在点C.求AP的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com