
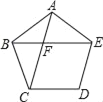
【题目】如图,在正五边形ABCDE中,对角线AC,BE相交于点F,F是线段BE、AC的黄金分割线吗?为什么?
【答案】见解析
【解析】
根据正五边形的性质得到∠ABC=∠BAE=108°,AB=BC=AE,则利用三角形内角和和等腰三角形的性质计算出∠BAC=∠BCA=36°,∠ABE=∠AEB=36°,易得∠CBF=72°,∠CFB=72°,所以CB=CF,再证明△ABF∽△ACB,则AB:AC=AF:AB,所以CF:AC=AF:CF,根据黄金分割的定义得到点F是线段AC的黄金分割点,用同样的方法可得F是线段BE的黄金分割点.
解:F是线段BE、AC的黄金分割点.理由如下:
∵五边形ABCDE是正五边形,
∴∠ABC=∠BAE=108°,AB=BC=AE,
∴∠BAC=∠BCA=36°,∠ABE=∠AEB=36°,
∴∠CBF=72°,∠CFB=72°,
∴CB=CF,
∵∠ABF=∠ACB=36°,
∴△ABF∽△ACB,
∴AB:AC=AF:AB,
∴CF:AC=AF:CF,
∴点F是线段AC的黄金分割点,
同理可得F是线段BE的黄金分割点.


 步步高达标卷系列答案
步步高达标卷系列答案科目:初中数学 来源: 题型:
【题目】当前,“校园ipad现象已经受到社会的广泛关注,某教学兴趣小组对”“是否赞成中学生带手机进校园”的问题进行了社会调查.小文将调查数据作出如下不完整的整理:
频数分布表
看法 | 频数 | 频率 |
赞成 | 5 | |
无所谓 | 0.1 | |
反对 | 40 | 0.8 |
(1)请求出共调查了多少人;并把小文整理的图表补充完整;
(2)小丽要将调查数据绘制成扇形统计图,则扇形图中“赞成”的圆心角是多少度?
(3)若该校有3000名学生,请您估计该校持“反对”态度的学生人数.

查看答案和解析>>
科目:初中数学 来源: 题型:
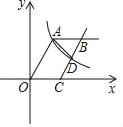
【题目】如图,在平面直角坐标系中,点A(2,4)在反比例函数y=![]() 的图象上,点C的坐标是(3,0),连接OA,过C作OA的平行线,过A作x轴的平行线,交于点B,BC与双曲线y=
的图象上,点C的坐标是(3,0),连接OA,过C作OA的平行线,过A作x轴的平行线,交于点B,BC与双曲线y=![]() 的图象交于D,连接AD.
的图象交于D,连接AD.
(1)求D点的坐标;
(2)四边形AOCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
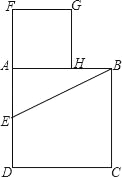
【题目】已知线段AB,按照如下的方法作图:以AB为边作正方形ABCD,取AD的中点E,连接EB,延长DA到F,使EF=EB,以线段AF为边,作正方形AFGH,那么点H是线段AB的黄金分割点吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线C1:y=ax2﹣4ax﹣5(a>0).
(1)当a=1时,求抛物线与x轴的交点坐标及对称轴;
(2)①试说明无论a为何值,抛物线C1一定经过两个定点,并求出这两个定点的坐标;
②将抛物线C1沿这两个定点所在直线翻折,得到抛物线C2,直接写出C2的表达式;
(3)若(2)中抛物线C2的顶点到x轴的距离为2,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠ACB=90°,AC=6cm,BC=8cm,动点P从点B出发,在BA边上以每秒5cm的速度向点A匀速运动,同时动点Q从点C出发,在CB边上以每秒4cm的速度向点B匀速运动,运动时间为t秒(0<t<2),连接PQ.

(1)若△BPQ与△ABC相似,求t的值;
(2)连接AQ、CP,若AQ⊥CP,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
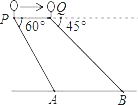
【题目】如图,一热气球在距地面90米高的P处,观测地面上点A的俯角为60°,气球以每秒9米的速度沿AB方向移动,5秒到达Q处,此时观测地面上点B的俯角为45°.(点P,Q,A,B在同一铅直面上).
(1)若气球从Q处继续向前移动,方向不变,再过几秒位于B点正上方?
(2)求AB的长(结果保留根号).
查看答案和解析>>
科目:初中数学 来源: 题型:
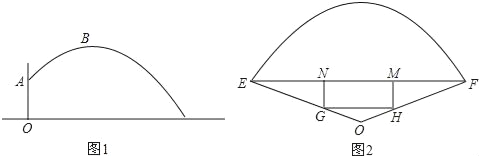
【题目】某公园在一个扇形OEF草坪上的圆心O处垂直于草坪的地上竖一根柱子OA,在A处安装一个自动喷水装置.喷头向外喷水.连喷头在内,柱高![]() m,水流在各个方向上沿形状相同的抛物线路径落下,喷出的水流在与D点的水平距离4米处达到最高点B,点B距离地面2米.当喷头A旋转120°时,这个草坪可以全被水覆盖.如图1所示.
m,水流在各个方向上沿形状相同的抛物线路径落下,喷出的水流在与D点的水平距离4米处达到最高点B,点B距离地面2米.当喷头A旋转120°时,这个草坪可以全被水覆盖.如图1所示.
(1)建立适当的坐标系,使A点的坐标为(O,![]() ),水流的最高点B的坐标为(4,2),求出此坐标系中抛物线水流对应的函数关系式;
),水流的最高点B的坐标为(4,2),求出此坐标系中抛物线水流对应的函数关系式;
(2)求喷水装置能喷灌的草坪的面积(结果用π表示);
(3)在扇形OEF的一块三角形区域地块△OEF中,现要建造一个矩形GHMN花坛,如图2的设计方案是使H、G分别在OF、OE上,MN在EF上.设MN=2x,当x取何值时,矩形GHMN花坛的面积最大?最大面积是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com