
【题目】投掷一枚质地均匀的正方体骰子.
(1)下列说法中正确的有 . (填序号)
①向上一面点数为1点和3点的可能性一样大;
②投掷6次,向上一面点数为1点的一定会出现1次;
③连续投掷2次,向上一面的点数之和不可能等于13.
(2)如果小明连续投掷了10次,其中有3次出现向上一面点数为6点,这时小明说:投掷正方体骰子,向上一面点数为6点的概率是![]() . 你同意他的说法吗?说说你的理由.
. 你同意他的说法吗?说说你的理由.
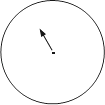
(3)为了估计投掷正方体骰子出现6点朝上的概率,小亮采用转盘来代替骰子做实验.下图是一个可以自由转动的转盘,请你将转盘分为2个扇形区域,分别涂上红、白两种颜色,使得转动转盘,当转盘停止转动后,指针落在红色区域的概率与投掷正方体骰子出现6点朝上的概率相同.(友情提醒:在转盘上用文字注明颜色和扇形圆心角的度数.)
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图1是一个新款水杯,水杯不盛水时按如图2所示的位置放置,这样可以快速晾干杯底,干净透气;将图2的主体部分的抽象成图3,此时杯口与水平直线的夹角35°,四边形ABCD可以看作矩形,测得AB=10cm,BC=8cm,过点A作AF⊥CE,交CE于点F. 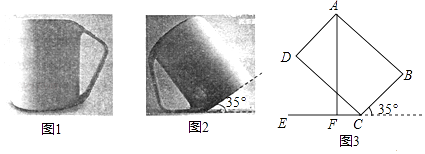
(1)求∠BAF的度数;(sin35°≈0.5736,cos35°≈0.8192,tan35°≈0.7002)
(2)求点A到水平直线CE的距离AF的长(精确到0.1cm)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,点E是BC的中点,连接并延长DE交AB的延长线于点F. 
(1)求证:△CDE≌△BFE;
(2)若CD=3cm,请求出AF的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,四边形ABCD四条边上的中点分别为E、F、G、H,顺次连接EF、FG、GH、HE,得到四边形EFGH(即四边形ABCD的中点四边形).
(1)四边形EFGH的形状是_____,
证明你的结论.
(2)当四边形ABCD的对角线满足_____条件时,四边形EFGH是矩形;
(3)当四边形ABCD的对角线满足_____条件时,四边形EFGH是菱形;
(4)你学过的哪种特殊四边形的中点四边形是矩形?_____;
(5)你学过的哪种特殊四边形的中点四边形是菱形?_____;
(6)你学过的哪种特殊四边形的中点四边形是正方形?_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,规定把一个点先绕原点逆时针旋转45°,再作出它关于原点的对称点称为一次变换,已知点A的坐标为(﹣2,0),把点A经过连续2014次这样的变换得到的点A2014的坐标是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)操作发现:
如图,在矩形ABCD中,E是BC的中点,将△ABE沿AE折叠后得到△AFE,点F在矩形ABCD内部,延长AF交CD于点G.猜想线段GF与GC有何数量关系?并证明你的结论.

(2)类比探究:
如图,将(1)中的矩形ABCD改为平行四边形,其它条件不变,(1)中的结论是否仍然成立?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
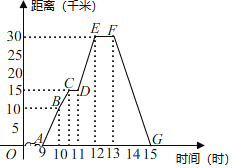
【题目】如图所示表示王勇同学骑自行车离家的距离与时间之间的关系,王勇9点离开家,15点回家,请结合图象,回答下列问题:
![]() 到达离家最远的地方是什么时间?离家多远?
到达离家最远的地方是什么时间?离家多远?
![]() 他一共休息了几次?休息时间最长的一次是多长时间?
他一共休息了几次?休息时间最长的一次是多长时间?
![]() 在哪些时间段内,他骑车的速度最快?最快速度是多少?
在哪些时间段内,他骑车的速度最快?最快速度是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】己知一元二次方程x2﹣3x+m﹣1=0.
(1)若方程有两个不相等的实数根,求实数m的取值范围;
(2)若方程有两个相等的实数根,求此时方程的根.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场销售每个进价为150元和120元的A、B两种型号的足球,如表是近两周的销售情况:
销售时段 | 销售数量 | 销售收入 | |
A种型号 | B种型号 | ||
第一周 | 3个 | 4个 | 1200元 |
第二周 | 5个 | 3个 | 1450元 |
![]() 进价、售价均保持不变,利润
进价、售价均保持不变,利润![]() 销售收入
销售收入![]() 进货成本
进货成本![]()
(1)求A、B两种型号的足球的销售单价;
(2)若商场准备用不多于8400元的金额再购进这两种型号的足球共60个,求A种型号的足球最多能采购多少个?
(3)在![]() 的条件下,商场销售完这60个足球能否实现利润超过2550元,若能,请给出相应的采购方案;若不能请说明理由.
的条件下,商场销售完这60个足球能否实现利润超过2550元,若能,请给出相应的采购方案;若不能请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com