
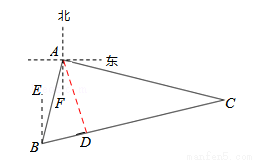
如图,轮船从点A处出发,先航行至位于点A的南偏西15°且点A相距100km的点B处,再航行至位于点A的南偏东75°且与点B相距200km的点C处.
(1)求点C与点A的距离(精确到1km);
(2)确定点C相对于点A的方向.
(参考数据: )
)

(1)173;(2)点C位于点A的南偏东75°方向.
【解析】
试题分析:(1)作辅助线,过点A作AD⊥BC于点D,构造直角三角形,解直角三角形即可.
(2)利用勾股定理的逆定理,判定△ABC为直角三角形;然后根据方向角的定义,即可确定点C相对于点A的方向.
试题解析:【解析】
(1)如答图,过点A作AD⊥BC于点D.
由图得,∠ABC=75°﹣10°=60°.
在Rt△ABD中,∵∠ABC=60°,AB=100,
∴BD=50,AD=50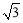 .
.
∴CD=BC﹣BD=200﹣50=150.
在Rt△ACD中,由勾股定理得:
AC=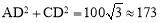 (km).
(km).
答:点C与点A的距离约为173km.
(2)在△ABC中,∵AB2+AC2=1002+(100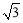 )2=40000,BC2=2002=40000,
)2=40000,BC2=2002=40000,
∴AB2+AC2=BC2. ∴∠BAC=90°.
∴∠CAF=∠BAC﹣∠BAF=90°﹣15°=75°.
答:点C位于点A的南偏东75°方向.
考点:1.解直角三角形的应用(方向角问题);2. 锐角三角函数定义;3.特殊角的三角函数值;4. 勾股定理和逆定理.


 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案科目:初中数学 来源:2014年初中毕业升学考试(江苏苏州卷)数学(解析版) 题型:选择题
如图,港口A在观测站O的正东方向,OA=4km.某船从港口A出发,沿北偏东15°方向航行一段距离后到达B处,此时从观测站O处测得该船位于北偏东60°的方向,则该船航行的距离(即AB的长)为( )

A.4km B.2 km C.2
km C.2 km D.(
km D.( +1)km
+1)km
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(江苏无锡卷)数学(解析版) 题型:解答题
三个小球分别标有﹣2,0,1三个数,这三个球除了标的数不同外,其余均相同,将小球放入一个不透明的布袋中搅匀.
(1)从布袋中任意摸出一个小球,将小球上所标之数记下,然后将小球放回袋中,搅匀后再任意摸出一个小球,再记下小球上所标之数,求两次记下之数的和大于0的概率.(请用“画树状图”或“列表”等方法给出分析过程,并求出结果)
(2)从布袋中任意摸出一个小球,将小球上所标之数记下,然后将小球放回袋中,搅匀后再任意摸出一个小球,将小球上所标之数再记下,…,这样一共摸了13次.若记下的13个数之和等于﹣4,平方和等于14.求:这13次摸球中,摸到球上所标之数是0的次数.
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(江苏无锡卷)数学(解析版) 题型:选择题
在直角坐标系中,一直线a向下平移3个单位后所得直线b经过点A(0,3),将直线b绕点A顺时针旋转60°后所得直线经过点B( ,0),则直线a的函数关系式为( )
,0),则直线a的函数关系式为( )
A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(江苏常州卷)数学(解析版) 题型:解答题
在平面直角坐标系xOy中,如图,已知Rt△DOE,∠DOE=90°,OD=3,点D在y轴上,点E在x轴上,在△ABC中,点A,C在x轴上,AC=5.∠ACB+∠ODE=180°,∠ABC=∠OED,BC=DE.按下列要求画图(保留作图痕迹):
(1)将△ODE绕O点按逆时针方向旋转90°得到△OMN(其中点D的对应点为点M,点E的对应点为点N),画出△OMN;
(2)将△ABC沿x轴向右平移得到△A′B′C′(其中点A,B,C的对应点分别为点A′,B′,C′),使得B′C′与(1)中的△OMN的边NM重合;
(3)求OE的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com