
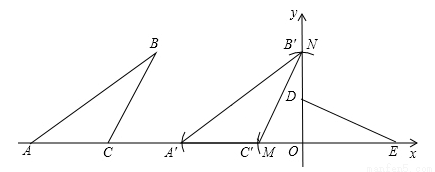
��ƽ��ֱ������ϵxOy�У���ͼ����֪Rt��DOE����DOE=90�㣬OD=3����D��y���ϣ���E��x���ϣ�����ABC�У���A��C��x���ϣ�AC=5����ACB+��ODE=180�㣬��ABC=��OED��BC=DE��������Ҫ��ͼ��������ͼ�ۼ�����
��1������ODE��O�㰴��ʱ�뷽����ת90��õ���OMN�����е�D�Ķ�Ӧ��Ϊ��M����E�Ķ�Ӧ��Ϊ��N����������OMN��
��2������ABC��x������ƽ�Ƶõ���A��B��C�䣨���е�A��B��C�Ķ�Ӧ��ֱ�Ϊ��A�䣬B�䣬C�䣩��ʹ��B��C���루1���е���OMN�ı�NM�غϣ�
��3����OE�ij���

��1����ͼ����������2����ͼ����������3��6.
��������
�����������1���Ե�OΪԲ�ģ���OEΪ�뾶��������y���������ཻ�ڵ�M����ODΪ�뾶��������x�Ḻ�����ཻ�ڵ�N������MN����.
��2����MΪԲ�ģ���AC��Ϊ�뾶������x�Ḻ�����ཻ�ڵ�A�䣬B����N�غϣ�C����M�غϣ�Ȼ��˳�����Ӽ���.
��3����OE=x����ON=x����MF��A��B���ڵ�F���жϳ�B��C��ƽ����A��B��O���ٸ��ݽ�ƽ�����ϵĵ㵽�ǵ����߾�����Ⱥͽ�ƽ���ߵĶԳ��Կɵ�B��F=B��O=OE=x��F C��=O C��=OD=3�����ù��ɶ�����ʽ���A��F��Ȼ���ʾ��A��B�䡢A��O����Rt��A��B��O�У����ù��ɶ����г�������⼴�ɣ�
�����������������
��1����OMN��ͼ��ʾ.
��2����A��B��C����ͼ��ʾ��
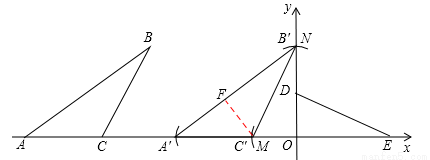
��3����OE=x����ON=x�����ͼ������M��MF��A��B���ڵ�F��
����ͼ��֪��B��C��ƽ����A��B��O����C��O��O B�䣬
��B��F=B��O=OE=x��F C��=O C��=OD=3��
��A��C��=AC=5����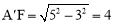 .��A��B��=x+4��A��O=5+3=8.
.��A��B��=x+4��A��O=5+3=8.
��Rt��A��B��O��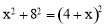 �����x=6.
�����x=6.
��OE=6��
���㣺1.��ͼ����ת��ƽ�Ʊ任����2.��ת��ƽ�Ʊ任�����ʣ�3.���ɶ�����4.����˼���Ӧ��.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ��2014����б�ҵ��ѧ���ԣ����ջ���������ѧ�������棩 ���ͣ�ѡ����
��ͼ��Բ��ĸ�߳�Ϊ2������Բ���ܳ�Ϊ3�����Բ�IJ����Ϊ��������

A��3�� B��3 C��6�� D��6
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014����б�ҵ��ѧ���ԣ��������ݾ�����ѧ�������棩 ���ͣ������
��ͼ���ִ��ӵ�A���������Ⱥ�����λ�ڵ�A����ƫ��15���ҵ�A���100km�ĵ�B�����ٺ�����λ�ڵ�A����ƫ��75�������B���200km�ĵ�C����
��1�����C���A�ľ��루��ȷ��1km����
��2��ȷ����C����ڵ�A�ķ���
���ο����ݣ� ��
��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014����б�ҵ��ѧ���ԣ��������ݾ�����ѧ�������棩 ���ͣ�ѡ����
��A��B��C��ͬһ�������ϣ����е�A��B��ʾ�����ֱ�Ϊ��3��1����BC=2����AC������ ��
A.3 B.2 C.3��5 D.2��6
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014����б�ҵ��ѧ���ԣ��������ݾ�����ѧ�������棩 ���ͣ�ѡ����
 ������ ��
������ ��
A. B.
B.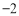 C.
C.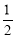 D.
D.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014����б�ҵ��ѧ���ԣ����ճ��ݾ�����ѧ�������棩 ���ͣ������
�ⲻ��ʽ��ͷ�ʽ���̣�
��1���ⲻ��ʽ�飺
��2�����ʽ���̣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014����б�ҵ��ѧ���ԣ����ճ��ݾ�����ѧ�������棩 ���ͣ������
��֪���εİ뾶Ϊ3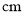 �������εĻ�����
�������εĻ�����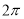
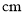 ��������ε�Բ�Ľǵ��� �ȣ����ε������ .(�������
��������ε�Բ�Ľǵ��� �ȣ����ε������ .(�������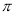 )
)
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014����б�ҵ��ѧ���ԣ�������Ǩ������ѧ�������棩 ���ͣ������
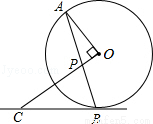
��ͼ��AB����O���ң�OP��OA��AB�ڵ�P������B��ֱ�߽�OP���ӳ����ڵ�C����CP=CB��
��1����֤��BC����O�����ߣ�
��2������O�İ뾶Ϊ ��OP=1����BC�ij���
��OP=1����BC�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014����б�ҵ��ѧ���ԣ������Ͼ�������ѧ�������棩 ���ͣ������
-2���෴���� ��-2�ľ���ֵ�� .
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com