
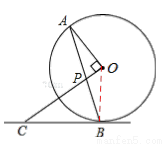
如图,AB是⊙O的弦,OP⊥OA交AB于点P,过点B的直线交OP的延长线于点C,且CP=CB.
(1)求证:BC是⊙O的切线;
(2)若⊙O的半径为 ,OP=1,求BC的长.
,OP=1,求BC的长.
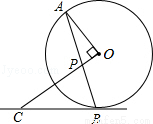
(1)证明见解析;(2)2.
【解析】
试题分析:(1)由垂直定义得∠A+∠APO=90°,根据等腰三角形的性质由CP=CB得∠CBP=∠CPB,根据对顶角相等得∠CPB=∠APO,即∠APO=∠CBP,而∠A=∠OBA,得∠OBC=∠CBP+∠OBA=∠APO+∠A=90°,然后根据切线的判定定理得到BC是⊙O的切线.
(2)设BC=x,则PC=x,在Rt△OBC中,根据勾股定理得到(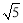 )2+x2=(x+1)2,然后解方程即可.
)2+x2=(x+1)2,然后解方程即可.
试题解析:【解析】
(1)证明:如答图,连接OB,
∵OP⊥OA,∴∠AOP=90°.∴∠A+∠APO=90°.
∵CP=CB,∴∠CBP=∠CPB.
∵∠CPB=∠APO,∴∠APO=∠CBP.
∵OA=OB,∴∠A=∠OBA.∴∠OBC=∠CBP+∠OBA=∠APO+∠A=90°.∴OB⊥BC.∴BC是⊙O的切线.
(2)设BC=x,则PC=x,
在Rt△OBC中,OB=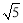 ,OC=CP+OP=x+1,
,OC=CP+OP=x+1,
∵OB2+BC2=OC2,∴(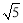 )2+x2=(x+1)2,解得x=2.
)2+x2=(x+1)2,解得x=2.
∴BC的长为2.
考点:1.等腰三角形的性质;2.切线的判定;3.勾股定理.


 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案科目:初中数学 来源:2014年初中毕业升学考试(江苏无锡卷)数学(解析版) 题型:选择题
在直角坐标系中,一直线a向下平移3个单位后所得直线b经过点A(0,3),将直线b绕点A顺时针旋转60°后所得直线经过点B( ,0),则直线a的函数关系式为( )
,0),则直线a的函数关系式为( )
A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(江苏常州卷)数学(解析版) 题型:解答题
在平面直角坐标系xOy中,如图,已知Rt△DOE,∠DOE=90°,OD=3,点D在y轴上,点E在x轴上,在△ABC中,点A,C在x轴上,AC=5.∠ACB+∠ODE=180°,∠ABC=∠OED,BC=DE.按下列要求画图(保留作图痕迹):
(1)将△ODE绕O点按逆时针方向旋转90°得到△OMN(其中点D的对应点为点M,点E的对应点为点N),画出△OMN;
(2)将△ABC沿x轴向右平移得到△A′B′C′(其中点A,B,C的对应点分别为点A′,B′,C′),使得B′C′与(1)中的△OMN的边NM重合;
(3)求OE的长.

查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(江苏常州卷)数学(解析版) 题型:选择题
甲,乙两人以相同路线前往距离单位10 的培训中心参加学习.图中
的培训中心参加学习.图中 分别表示甲,乙两人前往目的地所走的路程s
分别表示甲,乙两人前往目的地所走的路程s 随时间(分)变化的函数图象.以下说法:①乙比甲提前12分钟到达;②甲的平均速度为15千米/小时;③乙走了8
随时间(分)变化的函数图象.以下说法:①乙比甲提前12分钟到达;②甲的平均速度为15千米/小时;③乙走了8 后遇到甲;④乙出发6分钟后追上甲.其中正确的有( )
后遇到甲;④乙出发6分钟后追上甲.其中正确的有( )

A.4个 B.3个 C.2个 D.1个
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(江苏宿迁卷)数学(解析版) 题型:解答题
如图,已知抛物线y=ax2+bx+c(a>0,c<0)交x轴于点A,B,交y轴于点C,设过点A,B,C三点的圆与y轴的另一个交点为D.
(1)如图1,已知点A,B,C的坐标分别为(﹣2,0),(8,0),(0,﹣4);
①求此抛物线的表达式与点D的坐标;
②若点M为抛物线上的一动点,且位于第四象限,求△BDM面积的最大值;
(2)如图2,若a=1,求证:无论b,c取何值,点D均为定点,求出该定点坐标.

查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(江苏宿迁卷)数学(解析版) 题型:填空题
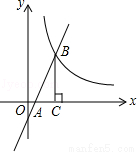
如图,一次函数y=kx﹣1的图象与x轴交于点A,与反比例函数 (x>0)的图象交于点B,BC垂直x轴于点C.若△ABC的面积为1,则k的值是 .
(x>0)的图象交于点B,BC垂直x轴于点C.若△ABC的面积为1,则k的值是 .
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(江苏南京卷)数学(解析版) 题型:解答题
如图,在△ABC中,D、E分别是AB、AC的中点,过点E作EF∥AB,交BC于点F.
(1)求证:四边形DBFE是平行四边形;
(2)当△ABC满足什么条件时,四边形DBEF是菱形?为什么?

查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(广西贺州卷)数学(解析版) 题型:选择题
A、B、C、D四名选手参加50米决赛,赛场共设1,2,3,4四条跑道,选手以随机抽签的方式决定各自的跑道,若A首先抽签,则A抽到1号跑道的概率是( )
A.1 B. C.
C. D.
D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com