
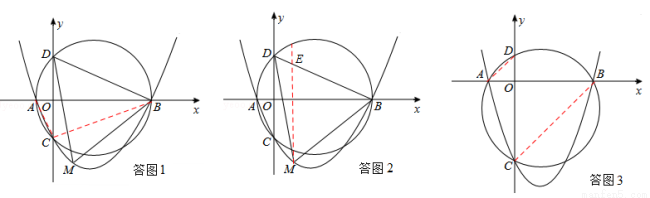
如图,已知抛物线y=ax2+bx+c(a>0,c<0)交x轴于点A,B,交y轴于点C,设过点A,B,C三点的圆与y轴的另一个交点为D.
(1)如图1,已知点A,B,C的坐标分别为(﹣2,0),(8,0),(0,﹣4);
①求此抛物线的表达式与点D的坐标;
②若点M为抛物线上的一动点,且位于第四象限,求△BDM面积的最大值;
(2)如图2,若a=1,求证:无论b,c取何值,点D均为定点,求出该定点坐标.

(1)①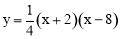 ,D(0,4);②36;(2)证明见解析,(0,1).
,D(0,4);②36;(2)证明见解析,(0,1).
【解析】
试题分析:(1)①利用待定系数法求抛物线的解析式;利用勾股定理的逆定理证明∠ACB=90°,由圆周角定理得AB为圆的直径,再由垂径定理知点C、D关于AB对称,由此得出点D的坐标.
②求出△BDM面积的表达式,再利用二次函数的性质求出最值.
(2)根据抛物线与x轴的交点坐标、根与系数的关系、相似三角形求解.
试题解析:【解析】
(1)①∵抛物线y=ax2+bx+c过点A(﹣2,0),B(8,0),
∴可设抛物线解析式为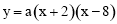 .
.
∵抛物线y=ax2+bx+c过点C(0,﹣4),
∴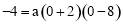 ,解得
,解得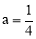 .
.
∴抛物线的解析式为: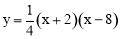 ,即
,即 .
.
∵OA=2,OB=8,OC=4,∴AB=10.
如答图1,连接AC、BC.
由勾股定理得:AC=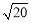 ,BC=
,BC=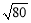 .
.
∵AC2+BC2=AB2=100,
∴∠ACB=90°.∴AB为圆的直径.
由垂径定理可知,点C、D关于直径AB对称,∴D(0,4).
②设直线BD的解析式为y=kx+b,
∵B(8,0),D(0,4),∴ ,解得
,解得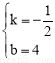 .∴直线BD解析式为:
.∴直线BD解析式为: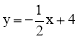 .
.
设M(x,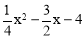 ),
),
如答图2,过点M作ME∥y轴,交BD于点E,则E(x,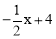 ).
).
∴ME=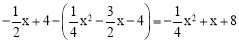 .
.
∴S△BDM=S△MED+S△MEB=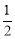 ME(xE﹣xD)+
ME(xE﹣xD)+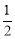 ME(xB﹣xD)=
ME(xB﹣xD)=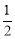 ME(xB﹣xD)=4ME.
ME(xB﹣xD)=4ME.
∴S△BDM=
∴当x=2时,△BDM的面积有最大值为36.
(2)证明:如答图3,连接AD、BC.
由圆周角定理得:∠ADO=∠CBO,∠DAO=∠BCO,
∴△AOD∽△COB.∴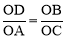 .
.
设A(x1,0),B(x2,0),
∵已知抛物线y=x2+bx+c(c<0),∴OC=﹣c,x1x2=c.
∴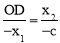 .∴
.∴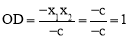 .
.
∴无论b,c取何值,点D均为定点,该定点坐标D(0,1).
考点:1.二次函数综合题;2.单动点问题;3.待定系数法的应用;4.曲线上点的坐标与方程的关系;5.勾股定理和逆定理;6.二次函数的性质;7.圆周角定理和垂径定理;8.相似三角形的判定和性质;9.一元二次方程根与系数的关系..


科目:初中数学 来源:2014年初中毕业升学考试(江苏常州卷)数学(解析版) 题型:填空题
已知扇形的半径为3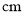 ,此扇形的弧长是
,此扇形的弧长是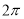
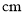 ,则此扇形的圆心角等于 度,扇形的面积是 .(结果保留
,则此扇形的圆心角等于 度,扇形的面积是 .(结果保留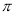 )
)
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(江苏常州卷)数学(解析版) 题型:选择题
已知两圆半径分别为3 ,5
,5 ,圆心距为7
,圆心距为7 ,则这两圆的位置关系为( )
,则这两圆的位置关系为( )
A.相交 B.外切 C.内切 D.外离
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(江苏宿迁卷)数学(解析版) 题型:解答题
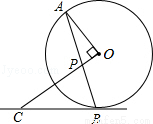
如图,AB是⊙O的弦,OP⊥OA交AB于点P,过点B的直线交OP的延长线于点C,且CP=CB.
(1)求证:BC是⊙O的切线;
(2)若⊙O的半径为 ,OP=1,求BC的长.
,OP=1,求BC的长.
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(江苏宿迁卷)数学(解析版) 题型:填空题
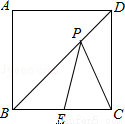
如图,正方形ABCD的边长为2,点E为边BC的中点,点P在对角线BD上移动,则PE+PC的最小值是 .
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(江苏南京卷)数学(解析版) 题型:解答题
已知二次函数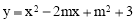 (m是常数)
(m是常数)
(1)求证:不论m为何值,该函数的图像与x轴没有公共点;
(2)把该函数的图像沿x轴向下平移多少个单位长度后,得到的函数的图像与x轴只有一个公共点?
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(广西贺州卷)数学(解析版) 题型:选择题
已知二次函数y=ax2+bx+c(a,b,c是常数,且a≠0)的图象如图所示,则一次函数 与反比例函数
与反比例函数 在同一坐标系内的大致图象是( )
在同一坐标系内的大致图象是( )

A. B.
B. C.
C. D.
D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com