
如图,在△ABC中,D、E分别是AB、AC的中点,过点E作EF∥AB,交BC于点F.
(1)求证:四边形DBFE是平行四边形;
(2)当△ABC满足什么条件时,四边形DBEF是菱形?为什么?

(1)证明见解析;(2)当AB=BC时,四边形DBEF是菱形,理由见解析.
【解析】
试题分析:(1)根据三角形的中位线平行于第三边并且等于第三边的一半可得DE∥BC,然后根据两组对边分别平行的四边形是平行四边形证明.
(2)根据邻边相等的平行四边形是菱形证明.
试题解析:(1)∵D、E分别是AB、AC的中点,∴DE是△ABC的中位线.∴DE∥BC.
又∵EF∥AB,∴四边形DBFE是平行四边形.
(2)当AB=BC时,四边形DBEF是菱形.理由如下:
∵D是AB的中点,∴BD=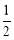 AB.
AB.
∵DE是△ABC的中位线,∴DE=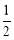 BC.
BC.
∵AB=BC,∴BD=DE.
又∵四边形DBFE是平行四边形,∴四边形DBFE是菱形.
考点:1.三角形中位线定理;2.平行四边形的判定;3.菱形的判定.


科目:初中数学 来源:2014年初中毕业升学考试(江苏徐州卷)数学(解析版) 题型:选择题
点A、B、C在同一条数轴上,其中点A、B表示的数分别为﹣3、1,若BC=2,则AC等于( )
A.3 B.2 C.3或5 D.2或6
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(江苏宿迁卷)数学(解析版) 题型:解答题
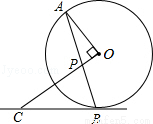
如图,AB是⊙O的弦,OP⊥OA交AB于点P,过点B的直线交OP的延长线于点C,且CP=CB.
(1)求证:BC是⊙O的切线;
(2)若⊙O的半径为 ,OP=1,求BC的长.
,OP=1,求BC的长.
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(江苏南京卷)数学(解析版) 题型:解答题
已知二次函数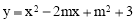 (m是常数)
(m是常数)
(1)求证:不论m为何值,该函数的图像与x轴没有公共点;
(2)把该函数的图像沿x轴向下平移多少个单位长度后,得到的函数的图像与x轴只有一个公共点?
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(江苏南京卷)数学(解析版) 题型:填空题
如图,沿一条母线将圆锥侧面剪开并展开,得到一个扇形,若圆锥底面圆半径r=2cm,扇形圆心角 ,则该圆锥母线长l为 cm.
,则该圆锥母线长l为 cm.
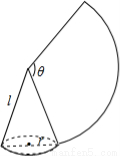
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(广西贺州卷)数学(解析版) 题型:填空题
如图,等腰△ABC中,AB=AC,∠DBC=15°,AB的垂直平分线MN交AC于点D,则∠A的度数是 .

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com