
【题目】如图,![]() 内接于
内接于![]() ,
,![]() 是弧
是弧![]() 的中点,
的中点,![]() 交
交![]() 于点
于点![]() ,且
,且![]() ,连接
,连接![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,连接
,连接![]() ,
,![]() 于
于![]() ,若
,若![]() ,
,![]() ,则
,则![]() ________.
________.
【答案】![]()
【解析】
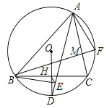
如图,延长BE交AC的延长线于N,连接OB、OC、BD.首先证明AB=AN,推出AB=8,再证明△OBD是等边三角形,推出∠BAC=60°,利用勾股定理分别求出BM、BC,再利用△AMF∽△BMC,得![]() =
=![]() ,即可解决问题.
,即可解决问题.
如图,延长BE交AC的延长线于N,连接OB、OC、BD.
∵![]() =
=![]() ,∴∠EAB=∠EAN.
,∴∠EAB=∠EAN.
∵AD⊥BN,∴∠AEB=∠AEN=90°,∴∠ABE+∠BAE=90°,∠N+∠EAN=90°,∴∠ABE=∠N,∴AB=AN,∴BE=EN.
∵OD⊥BC,∴BH=HC,∴CN=2EH=3,∴AB=AN=AC+CN=8.
∵OH=HD,BH⊥OD,∴BO=BD=OD,∴∠BOD=∠DOC=60°,∴∠BAC=![]() ∠BOC=60°.
∠BOC=60°.
∵BF⊥AC,∴∠AMB=90°,∴∠ABM=30°.在Rt△AMB中,AM=![]() AB=4,BM=4
AB=4,BM=4![]() .在Rt△BMC中,BC=
.在Rt△BMC中,BC=![]() =
=![]() =7.
=7.
∵∠MAF=∠MBC,∠AMF=∠BMC,∴△AMF∽△BMC,∴![]() =
=![]() ,∴
,∴![]() =
=![]() ,∴AF=
,∴AF=![]() .
.
故答案为:![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,∠MON=90°,矩形ABCD的顶点A、B分别在边OM,ON上,当B在边ON上运动时,A随之在OM上运动,矩形ABCD的形状保持不变,其中AB=2,BC=1,运动过程中,点D到点O的最大距离为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD的对角线AC,BD相交于点O,且DE∥AC,CE∥BD,若AC=2,则四边形OCED的周长为( )

A.16B.8C.4D.2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠B=90°,AB=12 米,BC=24 米,动点P从点A始沿边AB向B以2 米/秒的速度移动(不与点B重合),动点Q从点B开始沿边BC向C以4 米/秒的速度移动(不与点C重合).如果P、Q分别从A、B同时出发,设运动的时间为x 秒,四边形APQC的面积为y 米2.
(1)求y与x之间的函数关系式并写出自变量x的取值范围;
(2)四边形APQC的面积能否等于172米2.若能,求出运动的时间;若不能,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
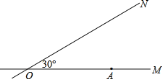
【题目】如图,![]() 、
、![]() 为相交成
为相交成![]() 度角的两条公路,在
度角的两条公路,在![]() 上距
上距![]() 点
点![]() 米有一所小学
米有一所小学![]() ,拖拉机沿
,拖拉机沿![]() 方向以每小时
方向以每小时![]() 千米的速度行驶,在小学周围
千米的速度行驶,在小学周围![]() 米范围内会受到拖拉机噪音的影响.试问小学是否会受到拖拉机噪音的影响?若受到影响,影响时间有多长?
米范围内会受到拖拉机噪音的影响.试问小学是否会受到拖拉机噪音的影响?若受到影响,影响时间有多长?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】操作发现:如图,已知△ABC和△ADE均为等腰三角形,AB=AC,AD=AE,将这两个三角形放置在一起,使点B,D,E在同一直线上,连接CE.

(1)如图1,若∠ABC=∠ACB=∠ADE=∠AED=55°,求证:△BAD≌△CAE;
(2)在(1)的条件下,求∠BEC的度数;
拓广探索:(3)如图2,若∠CAB=∠EAD=120°,BD=4,CF为△BCE中BE边上的高,请直接写出EF的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
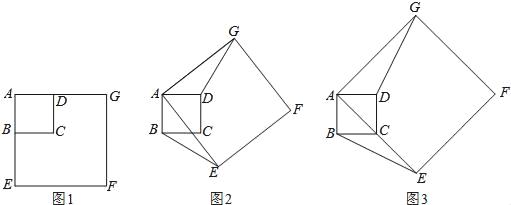
【题目】如图1,正方形ABCD与正方形AEFG的边AB、AE(AB<AE)在一条直线上,正方形AEFG以点A为旋转中心逆时针旋转,设旋转角为α.在旋转过程中,两个正方形只有点A重合,其它顶点均不重合,连接BE、DG.(1)当正方形AEFG旋转至如图2所示的位置时,求证:BE=DG;(2)如图3,如果α=45°,AB=2,AE=4![]() ,求点G到BE的距离.
,求点G到BE的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】张老师给爱好学习的小军和小俊提出这样一个问题:如图①,在△ABC中,AB=AC,点P为边BC上的任一点,过点P作PD⊥AB,PE⊥AC,垂足分别为D、E,过点C作CF⊥AB,垂足为F.求证:PD+PE=CF.
小军的证明思路是:如图2,连接AP,由△ABP与△ACP面积之和等于△ABC的面积可以证得:PD+PE=CF.
小俊的证明思路是:如图2,过点P作PG⊥CF,垂足为G,可以证得:PD=GF,PE=CG,则PD+PE=CF.

【变式探究】如图③,当点P在BC延长线上时,其余条件不变,求证:PD﹣PE=CF;请运用上述解答中所积累的经验和方法完成下题:
【结论运用】如图④,将矩形ABCD沿EF折叠,使点D落在点B上,点C落在点C′处,点P为折痕EF上的任一点,过点P作PG⊥BE、PH⊥BC,垂足分别为G、H,若AD=8,CF=3,求PG+PH的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com