Question

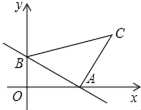
【题目】如图，经过原点的抛物线y=﹣x2+2mx（m＞0）与x轴的另一个交点为A．过点P（1，m）作直线PM⊥x轴于点M，交抛物线于点B．记点B关于抛物线对称轴的对称点为C（B、C不重合）．连接CB，CP．

（1）当m=3时，求点A的坐标及BC的长；
（2）当m＞1时，连接CA，问m为何值时CA⊥CP？
（3）过点P作PE⊥PC且PE=PC，问是否存在m，使得点E落在坐标轴上？若存在，求出所有满足要求的m的值，并定出相对应的点E坐标；若不存在，请说明理由．

Answer 1

【答案】
（1）

解：当m=3时，y=﹣x2+6x

令y=0得﹣x2+6x=0

∴x1=0，x2=6，

∴A（6，0）

当x=1时，y=5

∴B（1，5）

∵抛物线y=﹣x2+6x的对称轴为直线x=3

又∵B，C关于对称轴对称

∴BC=4

（2）

解：连接AC，过点C作CH⊥x轴于点H（如图1）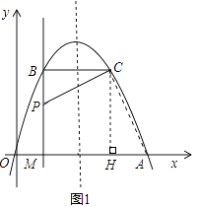

由已知得∠ACP=∠BCH=90°

∴∠ACH=∠PCB

又∵∠AHC=∠PBC=90°

∴△ACH∽△PCB，

∴ ，

∵抛物线y=﹣x2+2mx的对称轴为直线x=m，其中m＞1，

又∵B，C关于对称轴对称，

∴BC=2（m﹣1），

∵B（1，2m﹣1），P（1，m），

∴BP=m﹣1，

又∵A（2m，0），C（2m﹣1，2m﹣1），

∴H（2m﹣1，0），

∴AH=1，CH=2m﹣1，

∴ ，

∴m=

（3）

解：∵B，C不重合，∴m≠1，

（1.）当m＞1时，BC=2（m﹣1），PM=m，BP=m﹣1，

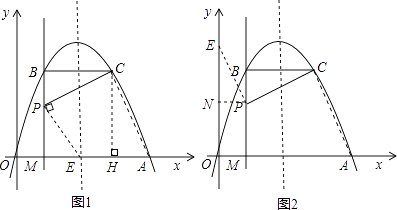
（i）若点E在x轴上（如图1），

∵∠CPE=90°，

∴∠MPE+∠BPC=∠MPE+∠MEP=90°，PC=EP，

在△BPC和△MEP中，

，

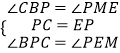∴△BPC≌△MEP，

∴BC=PM，

∴2（m﹣1）=m，

∴m=2，此时点E的坐标是（2，0）；

（ii）若点E在y轴上（如图2），

过点P作PN⊥y轴于点N，

易证△BPC≌△NPE，

∴BP=NP=OM=1，

∴m﹣1=1，

∴m=2，

此时点E的坐标是（0，4）；

（2.）当0＜m＜1时，BC=2（1﹣m），PM=m，BP=1﹣m，

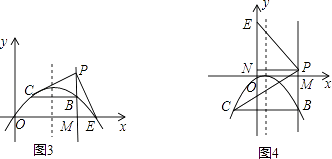
（i）若点E在x轴上（如图3），

易证△BPC≌△MEP，

∴BC=PM，

∴2（1﹣m）=m，

∴m= ，此时点E的坐标是（ ，0）；

（ii）若点E在y轴上（如图4），

过点P作PN⊥y轴于点N，

易证△BPC≌△NPE，

∴BP=NP=OM=1，

∴1﹣m=1，∴m=0（舍去），

综上所述，当m=2时，点E的坐标是（2，0）或（0，4），

当m= 时，点E的坐标是（ ，0）．

【解析】（1）把m=3，代入抛物线的解析式，令y=0解方程，得到的非0解即为和x轴交点的横坐标，再求出抛物线的对称轴方程，进而求出BC的长；（2）过点C作CH⊥x轴于点H（如图1）由已知得∠ACP=∠BCH=90°，利用已知条件证明△ACH∽△PCB，根据相似的性质得到： ，再用含有m的代数式表示出BC，CH，BP，代入比例式即可求出m的值；（3）存在，本题要分当m＞1时，BC=2（m﹣1），PM=m，BP=m﹣1和当0＜m＜1时，BC=2（1﹣m），PM=m，BP=1﹣m，两种情况分别讨论，再求出满足题意的m值和相对应的点E坐标．