
【题目】如图,四边形ABCD中,∠BAD=∠ADC=90°,AB=AD=2![]() ,CD=
,CD=![]() ,点P在四边形ABCD的边上.若P到BD的距离为
,点P在四边形ABCD的边上.若P到BD的距离为![]() ,则点P的个数为( )
,则点P的个数为( )

A.1B.2C.3D.4
【答案】B
【解析】
首先作出AB、AD边上的点P(点A)到BD的垂线段AE,即点P到BD的最长距离,作出BC、CD的点P(点C)到BD的垂线段CF,即点P到BD的最长距离,由已知计算出AE、CF的长与![]() 比较得出答案.
比较得出答案.
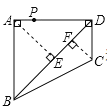 过点A作AE⊥BD于E,过点C作CF⊥BD于F,
过点A作AE⊥BD于E,过点C作CF⊥BD于F,
∵∠BAD=∠ADC=90°,AB=AD=2![]() ,CD=
,CD=![]() ,
,
∴∠ABD=∠ADB=45°,
∴∠CDF=90°∠ADB=45°,
∵sin∠ABD=![]() ,
,
∴AE=ABsin∠ABD=2![]() sin45
sin45
=![]()
![]() =2>
=2>![]() ,
,
所以在AB和AD边上有符合P到BD的距离为![]() 的点2个,
的点2个,
∵sin∠CDF=![]() ,
,
∴CF=CDsin∠CDF=![]()
![]() =1<
=1<![]() ,
,
所以在边BC和CD上没有到BD的距离为![]() 的点,
的点,
总之,P到BD的距离为![]() 的点有2个.
的点有2个.
故选:B.


科目:初中数学 来源: 题型:
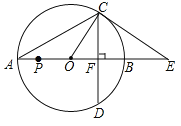
【题目】如图,以AB为直径的⊙O与CE相切于点C,CE交AB的延长线于点E,直径AB=18,∠A=30°,弦CD⊥AB,垂足为点F,连接AC,OC,则下列结论正确的是______.(写出所有正确结论的序号)
①![]() ;
;
②扇形OBC的面积为![]() π;
π;
③△OCF∽△OEC;
④若点P为线段OA上一动点,则APOP有最大值20.25.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题满分10分)如图,自来水厂A和村庄B在小河l的两侧,现要在A,B间铺设一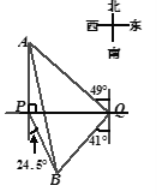 知输水管道.为了搞好工程预算,需测算出A,B间的距离.一小船在点P处测得A在正北方向,B位于南偏东24.5°方向,前行1200m,到达点Q处,测得A位于北偏东49°方向,B位于南偏西41°方向.
知输水管道.为了搞好工程预算,需测算出A,B间的距离.一小船在点P处测得A在正北方向,B位于南偏东24.5°方向,前行1200m,到达点Q处,测得A位于北偏东49°方向,B位于南偏西41°方向.
(1)线段BQ与PQ是否相等?请说明理由;
(2)求A,B间的距离.(参考数据cos41°=0.75)
查看答案和解析>>
科目:初中数学 来源: 题型:
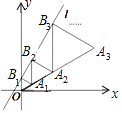
【题目】如图,在平面直角坐标系中,直线l:y=![]() 与y轴交于点B1,以OB1为一边在OB1右侧作等边三角形A1OB1,过点A1作A1B2平行于y轴,交直线l于点B2,以A1B2为一边在A1B2右侧作等边三角形A2A1B2,过点A2作A2B3平行于y轴,交直线l于点B3,以A2B3为一边在A2B3右侧作等边三角形A3A2B3,……则点A2019的纵坐标是( )
与y轴交于点B1,以OB1为一边在OB1右侧作等边三角形A1OB1,过点A1作A1B2平行于y轴,交直线l于点B2,以A1B2为一边在A1B2右侧作等边三角形A2A1B2,过点A2作A2B3平行于y轴,交直线l于点B3,以A2B3为一边在A2B3右侧作等边三角形A3A2B3,……则点A2019的纵坐标是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,∠BAC的平分线交BC于点D,点O在AB上,以点O为圆心,OA为半径的圆恰好经过点D,分别交AC、AB于点E. F.
(1)试判断直线BC与⊙O的位置关系,并说明理由;
(2)若BD=2![]() ,BF=2,求⊙O的半径.
,BF=2,求⊙O的半径.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠A=90°,AB=2cm,AC=4cm.动点P从点A出发,沿AB方向以1cm/s的速度向点B运动,动点Q从点B同时出发,沿BA方向以1cm/s的速度向点A运动.当点P到达点B时,P,Q两点同时停止运动,以AP为一边向上作正方形APDE,过点Q作QF∥BC,交AC于点F.设点P的运动时间为ts,正方形和梯形重合部分的面积为Scm2.
(1)当t= _________ s时,点P与点Q重合;
(2)当t= _________ s时,点D在QF上;
(3)当点P在Q,B两点之间(不包括Q,B两点)时,求S与t之间的函数关系式.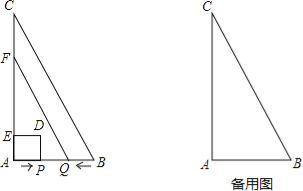
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了倡导节约用电,某市将实行居民生活用电阶梯电价方案,图中折线反映了每户每月用电电费y(元)与用电量x(度)间的函数关系式。
(1)根据图象,阶梯电价方案分为三个档次,填写下表:

(2)求每月用电量为100度时所需交的电费:
(3)第二档每用电费y(元)与用电量(度)间的函数关系式;
(4)在每月用电量超过230度时,每多用1度电要比第二档多付电费m元,小刚家某月用电310度,交电费168元,求m的值
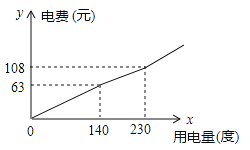
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与
与![]() 轴的一个交点为
轴的一个交点为![]() ,与
,与![]() 轴的交点
轴的交点![]() 在点
在点![]() 与点
与点![]() 之间(包含端点),顶点
之间(包含端点),顶点![]() 的坐标为
的坐标为![]() 。则下列结论:①
。则下列结论:①![]() ;②
;②![]() ;③对于任意实数
;③对于任意实数![]() ,
,![]() 总成立;④关于
总成立;④关于![]() 的方程
的方程![]() 没有实数根。其中结论正确的个数为()
没有实数根。其中结论正确的个数为()

A.![]() 个B.
个B.![]() 个C.
个C.![]() 个D.
个D.![]() 个
个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() 开口向下,与
开口向下,与![]() 轴交于点
轴交于点![]() ,顶点坐标为
,顶点坐标为![]() ,与
,与![]() 轴的交点在
轴的交点在![]() ,
,![]() 之间(包含端点),则下列结论:
之间(包含端点),则下列结论:
①![]() ;②
;②![]() ;③对于任意实数
;③对于任意实数![]() ,
,![]() 总成立;
总成立;
④关于![]() 的方程
的方程![]() 有两个不相等的实数根.
有两个不相等的实数根.
其中结论正确的个数是( )
A. 1个B. 2个
C. 3个D. 4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com