
分析 把原方程②进行变形,化为(x2+3x)+(x+y)=14,令x2+3x=a,x+y=b,根据题意得到一元二次方程,求出a、b,构造方程组求解即可.
解答 解:原方程组可化为$\left\{\begin{array}{l}{({x}^{2}+3x)(x+y)=40}\\{({x}^{2}+3x)+(x+y)=14}\end{array}\right.$,
令x2+3x=a,x+y=b,则ab=40,a+b=14,
∴a、b是方程t2-14t+40=0的两个根,
解得$\left\{\begin{array}{l}{a=10}\\{b=4}\end{array}\right.$或$\left\{\begin{array}{l}{a=4}\\{b=10}\end{array}\right.$,
于是$\left\{\begin{array}{l}{{x}^{2}+3x=10}\\{x+y=4}\end{array}\right.$或$\left\{\begin{array}{l}{{x}^{2}+3x=4}\\{x+y=10}\end{array}\right.$,
分别求解,得原方程组的解为$\left\{\begin{array}{l}{{x}_{1}=2}\\{{y}_{1}=2}\end{array}\right.$,$\left\{\begin{array}{l}{{x}_{2}=-5}\\{{y}_{2}=9}\end{array}\right.$,$\left\{\begin{array}{l}{{x}_{3}=1}\\{{y}_{3}=9}\end{array}\right.$,$\left\{\begin{array}{l}{{x}_{4}=-4}\\{{y}_{4}=14}\end{array}\right.$.
点评 本题考查的是高次方程的解法,把原方程组进行正确的变形是解题的关键,解高次方程时,要灵活运用换元法,使方程降次,然后再解.


 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案科目:初中数学 来源: 题型:填空题
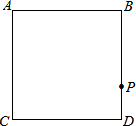 已知四边形ACDB为正方形,P是正方形边上任意一点,若P运动的方向为逆时针运动,
已知四边形ACDB为正方形,P是正方形边上任意一点,若P运动的方向为逆时针运动,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
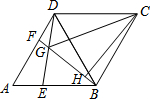 如图,△ADB、△BCD都是等边三角形,点E,F分别是AB,AD上两个动点,满足AE=DF.连接BF与DE相交于点G,CH⊥BF,垂足为H,连接CG.若DG=a,BG=b,且a、b满足下列关系:a2+b2=5,ab=2,则GH=$\frac{3}{2}$.
如图,△ADB、△BCD都是等边三角形,点E,F分别是AB,AD上两个动点,满足AE=DF.连接BF与DE相交于点G,CH⊥BF,垂足为H,连接CG.若DG=a,BG=b,且a、b满足下列关系:a2+b2=5,ab=2,则GH=$\frac{3}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,C为线段AE上一动点(不与点A,E重合),在AE同侧分别作正△ABC和正△CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连结PQ.以下五个结论:①AD=BE;②PQ∥AE;③AC=BQ;④DE=DP;⑤CP=CQ;⑥∠AOB=60°.
如图,C为线段AE上一动点(不与点A,E重合),在AE同侧分别作正△ABC和正△CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连结PQ.以下五个结论:①AD=BE;②PQ∥AE;③AC=BQ;④DE=DP;⑤CP=CQ;⑥∠AOB=60°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在一次数学活动课上,老师将一块等腰直角三角形纸片PMN的直角顶点P放在正方形ABCD的对角线BD上,使直角边PM经过正方形的顶点C,另一直角边PN与AB交于点E,如图所示,问:CE和MN存在怎样的位置关系.
在一次数学活动课上,老师将一块等腰直角三角形纸片PMN的直角顶点P放在正方形ABCD的对角线BD上,使直角边PM经过正方形的顶点C,另一直角边PN与AB交于点E,如图所示,问:CE和MN存在怎样的位置关系.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
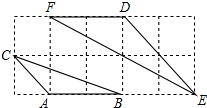 如图,如果△ABC与△DEF都是正方形网格中的格点三角形(顶点在格点上),那么△DEF与△ABC的周长比为( )
如图,如果△ABC与△DEF都是正方形网格中的格点三角形(顶点在格点上),那么△DEF与△ABC的周长比为( )| A. | 4:1 | B. | 3:1 | C. | 2:1 | D. | $\sqrt{2}$:1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com