
【题目】如图(1),在△OBC中,点A是BO延长线上的一点,
(1)![]() , Q是BC边上一点,连结AQ交OC边于点P,如图(2),若
, Q是BC边上一点,连结AQ交OC边于点P,如图(2),若![]() = .猜测:
= .猜测: ![]() 的大小关系是 ;
的大小关系是 ;
(2)将图(2)中的CO延长到点D,AQ延长到点E,连结DE,得到图(3),则![]() 等于图中哪三个角的和?并说明理由;
等于图中哪三个角的和?并说明理由;
(3)求图(3)中![]() 的度数.
的度数.

【答案】(1)78;96;∠A+∠B+∠C=∠OPQ; (2)∠AQB=∠C+∠D+∠E;(3)180°.
【解析】试题分析:(1)根据三角形外角的性质即可求得∠AOC=![]() ;根据三角形外角的性质可得∠AQC=∠A+∠B, ∠AQC +∠C=∠OPQ,即可得∠A+∠B+∠C=∠OPQ;(2) ∠AQB=∠C+∠D+∠E,根据三角形外角的性质即可证得结论;(3) 根据三角形外角的性质可得∠AQC=∠A+∠B,∠QPC=∠D+∠E,再由三角形的内角和定理可得∠AQC+∠QPC+∠C=180°,从而求得∠A+∠D+∠B+∠E+∠C=180°.
;根据三角形外角的性质可得∠AQC=∠A+∠B, ∠AQC +∠C=∠OPQ,即可得∠A+∠B+∠C=∠OPQ;(2) ∠AQB=∠C+∠D+∠E,根据三角形外角的性质即可证得结论;(3) 根据三角形外角的性质可得∠AQC=∠A+∠B,∠QPC=∠D+∠E,再由三角形的内角和定理可得∠AQC+∠QPC+∠C=180°,从而求得∠A+∠D+∠B+∠E+∠C=180°.
试题解析:
(1)78;96;∠A+∠B+∠C=∠OPQ;
(2)∠AQB=∠C+∠D+∠E,
理由是:∵∠EPC=∠D+∠E,∠AQB=∠C+∠EPC,
∴∠AQB=∠C+∠D+∠E;
(3)∵∠AQC=∠A+∠B,∠QPC=∠D+∠E,
又∵∠AQC+∠QPC+∠C=180°,
∴∠A+∠B+∠D+∠E+∠C=180°
即∠A+∠D+∠B+∠E+∠C=180°.
点睛:本题主要考查了三角形外角的性质及三角形的内角和定理,熟知三角形的一个外角等于不相邻的两个内角的和是解题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,已知反比例函数y=kx-1(k>0)的图象与一次函数图象y=﹣x+4交于a、b两点,点a的纵坐标为3.
(1)求反比例函数的解析;
(2)y轴上是否存在一点P,使2∠APB=∠AOB?若存在,求出点P的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:A=2a2+3ab﹣2a﹣1,B=﹣a2+ab+1
(1)当a=﹣1,b=2时,求A+2B的值;
(2)若(1)中的代数式的值与a的取值无关,求b的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义一种新运算:观察下列各式:
1⊙3=1×4+3=7 3⊙(﹣1)=3×4﹣1=11 5⊙4=5×4+4=24 4⊙(﹣3)=4×4﹣3=13
(1)请你想一想:a⊙b= ;
(2)若a≠b,那么a⊙b b⊙a(填入“=”或“≠”)
(3)若a⊙(﹣2b)=4,则2a﹣b= ;请计算(a﹣b)⊙(2a+b)的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一辆慢车与一辆快车分别从甲、乙两地同时出发,匀速相向而行,两车在途中相遇后都停留一段时间,然后分别按原速一同驶往甲地后停车.设慢车行驶的时间为x小时,两车之间的距离为y千米,图中折线表示y与x之间的函数图象,请根据图象解决下列问题: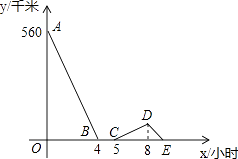
(1)甲乙两地之间的距离为千米;
(2)求快车和慢车的速度;
(3)求线段DE所表示的y与x之间的函数关系式,并写出自变量x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某玩具厂生产一种玩具,本着控制固定成本,降价促销的原则,使生产的玩具能够全部售出.据市场调查,若按每个玩具280元销售时,每月可销售300个.若销售单价每降低1元,每月可多售出2个.据统计,每个玩具的固定成本Q(元)与月产销量y(个)满足如下关系:
月产销量y(个) | … | 160 | 200 | 240 | 300 | … |
每个玩具的固定成本Q(元) | … | 60 | 48 | 40 | 32 | … |
(1)写出月产销量y(个)与销售单价x (元)之间的函数关系式;
(2)求每个玩具的固定成本Q(元)与月产销量y(个)之间的函数关系式;
(3)若每个玩具的固定成本为30元,则它占销售单价的几分之几?
(4)若该厂这种玩具的月产销量不超过400个,则每个玩具的固定成本至少为多少元?销售单价最低为多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com