
【题目】如图,四边形ABCD是平行四边形,点E是边CD上一点,且BC=EC,CF⊥BE交AB于点F,P是EB延长线上一点,下列结论:①BE平分∠CBF;②CF平分∠DCB;③BC=FB;④PF=PC.其中正确结论的个数为( )
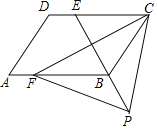
A.1B.2C.3D.4
科目:初中数学 来源: 题型:
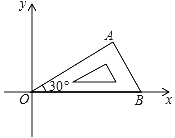
【题目】将含有 30°角的直角三角板 OAB 如图放置在平面直角坐标系中,OB 在 x轴上,若 OA=2,将三角板绕原点 O 顺时针旋转 75°,则点 A 的对应点 A′ 的坐标为___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
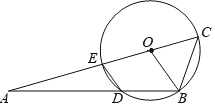
【题目】如图,以△AOB 的顶点 O 为圆心,OB 为半径作⊙O,交 OA 于点 E,交 AB 于点 D,连接 DE,DE∥OB,延长 AO 交⊙O 于点 C,连接 CB.
(1)求证:![]() ;
;
(2)若 AD=4![]() ,AE=CE,求 OC 的长.
,AE=CE,求 OC 的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】红树林学校在七年级新生中举行了全员参加的“防溺水”安全知识竞赛,试卷题目共10题,每题10分.现分别从三个班中各随机取10名同学的成绩(单位:分),收集数据如下:
1班:90,70,80,80,80,80,80,90,80,100;
2班:70,80,80,80,60,90,90,90,100,90;
3班:90,60,70,80,80,80,80,90,100,100.
整理数据:
分数 人数 班级 | 60 | 70 | 80 | 90 | 100 |
1班 | 0 | 1 | 6 | 2 | 1 |
2班 | 1 | 1 | 3 |
| 1 |
3班 | 1 | 1 | 4 | 2 | 2 |
分析数据:
平均数 | 中位数 | 众数 | |
1班 | 83 | 80 | 80 |
2班 | 83 |
|
|
3班 |
| 80 | 80 |
根据以上信息回答下列问题:
(1)请直接写出表格中![]() 的值;
的值;
(2)比较这三组样本数据的平均数、中位数和众数,你认为哪个班的成绩比较好?请说明理由;
(3)为了让学生重视安全知识的学习,学校将给竞赛成绩满分的同学颁发奖状,该校七年级新生共570人,试估计需要准备多少张奖状?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】金桔是浏阳的特色水果,金桔一上市,水果店的老板就用1200元购进一批金桔,很快售完,老板又用2500元购进第二批金桔,所购件数是第一批的2倍,但进价比第一批每件多了5元.
(1)第一批金桔每件进价为多少元?
(2)水果店老板销售这两批金桔时,每件售价都是150元,当第二批金桔售出80%后,决定打七折促销,结果全部售完,水果店老板共盈利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
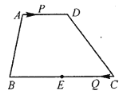
【题目】如图,在四边形![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() 是
是![]() 的中点.点
的中点.点![]() 以每秒1个单位长度的速度从点
以每秒1个单位长度的速度从点![]() 出发,沿
出发,沿![]() 向点
向点![]() 运动;同时,点
运动;同时,点![]() 以每秒2个单位长度的速度从点
以每秒2个单位长度的速度从点![]() 出发,沿
出发,沿![]() 向点
向点![]() 运动.点
运动.点![]() 停止运动时,点
停止运动时,点![]() 也随之停止运动.求当运动时间
也随之停止运动.求当运动时间![]() 为多少秒时,以点
为多少秒时,以点![]() ,
,![]() ,
,![]() ,
,![]() 为顶点的四边形是平行四边形.
为顶点的四边形是平行四边形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着车辆的增加,交通违规的现象越来越严重,交警对某雷达测速区检测到的一组汽车的时速数据进行整理,得到其频数及频率如表(未完成):
数据段 | 频数 | 频率 |
30~40 | 10 | 0.05 |
40~50 | 36 | |
50~60 | 0.39 | |
60~70 | ||
70~80 | 20 | 0.10 |
总计 | 200 | 1 |
注:30~40为时速大于等于30千米而小于40千米,其他类同
(1)请你把表中的数据填写完整;
(2)补全频数分布直方图;
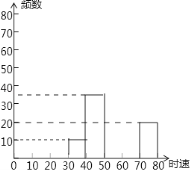
(3)如果汽车时速不低于60千米即为违章,则违章车辆共有多少辆?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象相交于第一、象限内的
的图象相交于第一、象限内的![]() ,
,![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() .
.
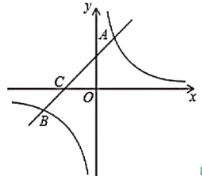
(1)求该反比例函数和一次函数的解析式;
(2)直接写出当![]() 时,
时,![]() 的取值范围;
的取值范围;
(3)长为2的线段![]() 在射线
在射线![]() 上左右移动,若射线
上左右移动,若射线![]() 上存在三个点
上存在三个点![]() 使得
使得![]() 为等腰三角形,求
为等腰三角形,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
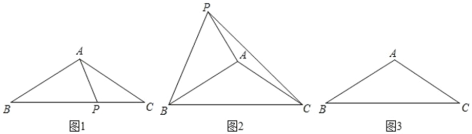
【题目】等腰△ABC 中,AB=AC,∠BAC=120°,点 P 为平面内一点.
(1)如图 1,当点 P 在边 BC 上时,且满足∠APC=120°,求![]() 的值;
的值;
(2)如图 2,当点 P 在△ABC 的外部,且满足∠APC+∠BPC=90°,求证:BP=![]() AP;
AP;
(3)如图 3,点 P 满足∠APC=60°,连接 BP,若 AP=1,PC=3,直接写出BP 的长度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com