
【题目】如图,在平面直角坐标系中,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象相交于第一、象限内的
的图象相交于第一、象限内的![]() ,
,![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() .
.
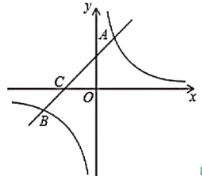
(1)求该反比例函数和一次函数的解析式;
(2)直接写出当![]() 时,
时,![]() 的取值范围;
的取值范围;
(3)长为2的线段![]() 在射线
在射线![]() 上左右移动,若射线
上左右移动,若射线![]() 上存在三个点
上存在三个点![]() 使得
使得![]() 为等腰三角形,求
为等腰三角形,求![]() 的值.
的值.
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() 或
或![]() ;(3)
;(3)![]() -1
-1
【解析】
(1)利用待定系数法即可解决问题.
(2)利用图象法,写出y1D的图象在y2的图象上方的对应的自变量的取值即可.
(3)如图2中,分别以E,F为圆心EF为半径画圆,两圆在EF的上方交于点N,当点N在射线CA上时,射线CA上存在三个点P使得△PEF为等腰三角形.解直角三角形求出CH,EH即可.
解:(1)∵A(3,5),B(a,-3)在![]() 的图象上,
的图象上,
∴m=15,a=-5,
∴A(3,5),B(-5,-3),
把A,B的坐标代入y1=kx+b中,
得![]() ,解得:
,解得: ![]()
![]()
(2)观察图1可知:当y1>y2时,x的取值范围为:x>3或-5<x<0.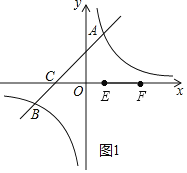
(3)如图2中,分别以E,F为圆心EF为半径画圆,两圆在EF的上方交于点N,当点N在射线CA上时,射线CA上存在三个点P使得△PEF为等腰三角形.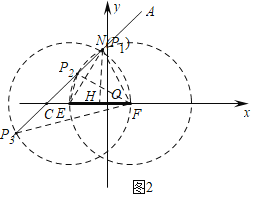
作NH⊥EF于H.
∵NE=EF=NF,NH⊥EF,
∴EH=HF=1,NH=![]() ,
,
∵直线AC的解析式为y=x+2,
∴∠ACF=45°,
∴CH=NH=![]() ,
,
∴EC=CH-EH=![]() -1
-1


 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,分别以AB、AD为边向外作等边△ABE、△ADF,延长CB交AE于点G,点G在点A、E之间,连接CE、CF,EF,则以下四个结论一定正确的是:①△CDF≌△EBC;②∠CDF=∠EAF;③△ECF是等边△;④CG⊥AE( )
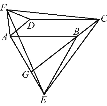
A. 只有①② B. 只有①②③ C. 只有③④ D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是平行四边形,点E是边CD上一点,且BC=EC,CF⊥BE交AB于点F,P是EB延长线上一点,下列结论:①BE平分∠CBF;②CF平分∠DCB;③BC=FB;④PF=PC.其中正确结论的个数为( )
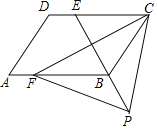
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小王是“新星厂”的一名工人,请你阅读下列信息:
信息一:工人工作时间:每天上午8:00—12:00,下午14:00—18:00,每月工作25天;
信息二:小王生产甲、乙两种产品的件数与所用时间的关系见下表:
生产甲种产品数(件) | 生产乙种产品数(件) | 所用时间(分钟) |
10 | 10 | 350 |
30 | 20 | 850 |
信息三:按件计酬,每生产一件甲种产品得1.50元,每生产一件乙种产品得2.80元;
信息四:该厂工人每月收入由底薪和计酬工资两部分构成,小王每月的底薪为1900元.请根据以上信息,解答下列问题:
(1)小王每生产一件甲种产品和一件乙种产品分别需要多少分钟;
(2)2018年1月工厂要求小王生产甲种产品的件数不少于60件,则小王该月收入最多是多少元?此时小王生产的甲、乙两种产品分别是多少件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在学校组织的“学习强国”阅读知识竞赛中,每班参加比赛的人数相同,成绩分为![]() 四个等级,其中相应等级的得分依次记为
四个等级,其中相应等级的得分依次记为![]() 分,
分,![]() 分,
分,![]() 分和
分和![]() 分.年级组长张老师将班
分.年级组长张老师将班![]() 和
和![]() 班的成绩进行整理并绘制成如下的统计图:
班的成绩进行整理并绘制成如下的统计图:
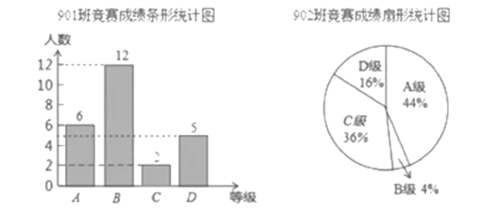
(1)在本次竞赛中,![]() 班
班![]() 级及以上的人数有多少?
级及以上的人数有多少?
(2)请你将下面的表格补充完整:
平均数(分) | 中位数(分) | 众数(分) |
| |
|
|
|
| |
|
|
|
|
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知:在△ABC中,AB、BC边上的垂直平分线相交于点P.若∠BAC=50°,则∠BPC的度数为( )
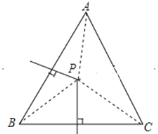
A.100°B.110°C.115°D.120°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知点A(0,4),△AOB为等边三角形,P是x轴负半轴上一个动点(不与原点O重合),以线段AP为一边在其右侧作等边三角形△APQ.
(1)求点B的坐标;
(2)在点P的运动过程中,∠ABQ的大小是否发生改变?如不改变,求出其大小;如改变,请说明理由;
(3)连接OQ,当OQ∥AB时,求点P的坐标.
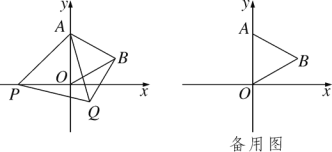
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(8分)某中学数学活动小组为了调查居民的用水情况,从某社区的![]() 户家庭中随机抽取了
户家庭中随机抽取了![]() 户家庭的月用水量,结果如下表所示:
户家庭的月用水量,结果如下表所示:
月用水量(吨) |
|
|
|
|
|
|
|
户数 |
|
|
|
|
|
|
|
(1)求这![]() 户家庭月用水量的平均数、众数和中位数;
户家庭月用水量的平均数、众数和中位数;
(2)根据上述数据,试估计该社区的月用水量;
(3)由于我国水资源缺乏,许多城市常利用分段计费的办法引导人们节约用水,即规定每个家庭的月基本用水量为![]() (吨),家庭月用水量不超过
(吨),家庭月用水量不超过![]() (吨)的部分按原价收费,超过
(吨)的部分按原价收费,超过![]() (吨)的部分加倍收费.你认为上述问题中的平均数、众数和中位数中哪一个量作为月基本用水量比较合理?简述理由.
(吨)的部分加倍收费.你认为上述问题中的平均数、众数和中位数中哪一个量作为月基本用水量比较合理?简述理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在四边形ABCD中,AB=CD,AD=BC,点E在CD上,连接AE并延长,交BC的延长线于F.
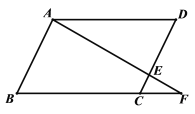
(1)求证:△ADE∽△FCE;
(2)若AB=4,AD=6,CF=2,求DE的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com