
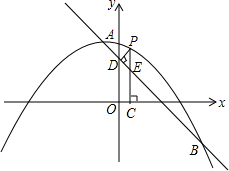
 如图,在直角坐标系中,直线y=-x+k经过抛物线y=ax2+bx+c的顶点A(-1,5)和另一点B(8,-4).
如图,在直角坐标系中,直线y=-x+k经过抛物线y=ax2+bx+c的顶点A(-1,5)和另一点B(8,-4).分析 (1)利用顶点式假设出二次函数解析式进而得出a,k的值;
(2)①得出Rt△PDE∽Rt△GOK,进而利用相似三角形的性质得出L与x之间的函数关系式;
②设点P坐标为(x,y),若存在,则点P在第一象限的角平分线上,则有x=y,进而得出x的值即可得出P点坐标.
解答 解:(1)依题意可设抛物线的解析式为:y=a(x+1)2+5,
∴-4=a(8+1)2+5.
∴a=-$\frac{1}{9}$,
∴抛物线y=-$\frac{1}{9}$(x+1)2+5.
即y=-$\frac{1}{9}$x2-$\frac{2}{9}$x+$\frac{44}{9}$.
∵直线y=-x+k过点A(-1,5),
则5=1+k
解得:k=4;
(2)①设直线解析式为y=-x+k与坐标轴交于G,K两点,
则G(0,4),K(4,0).
∴∠GKO=45°,GK=$\sqrt{{4}^{2}+{4}^{2}}$=4$\sqrt{2}$.
∴Rt△ECK中,EC=CK=4-x.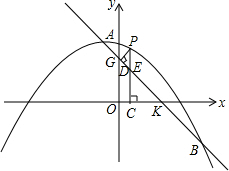
∴PE=PC-EC=y-x.
由题意,知Rt△PDE∽Rt△GOK,
∴$\frac{PE}{GK}$=$\frac{L}{8+4\sqrt{2}}$,
∴$\frac{y-x}{4\sqrt{2}}$=$\frac{L}{8+4\sqrt{2}}$,
∴L=$\frac{(y-x)(8+4\sqrt{2})}{4\sqrt{2}}$
=(y-x)($\sqrt{2}+$1),
=-$\frac{1}{9}$x2-$\frac{2}{9}$x+$\frac{44}{9}$-x)($\sqrt{2}+1$),
=-$\frac{\sqrt{2}-1}{9}$x2-$\frac{11(\sqrt{2}+1)}{9}$x+$\frac{44}{9}$($\sqrt{2}+1$),
②存在.
设点P坐标为(x,y),若存在,则点P在第一象限的角平分线上,则有x=y,
∴x=-$\frac{1}{9}$(x+1)2+5,
解得:x=$\frac{-11±\sqrt{121+176}}{2}$=$\frac{-11±\sqrt{297}}{2}$,
∵P在第一象限,
∴x=$\frac{-11+\sqrt{297}}{2}$,
∴P为($\frac{-11+\sqrt{297}}{2}$,$\frac{-11+\sqrt{297}}{2}$).
点评 此题主要考查了二次函数的综合题型,其中涉及到的知识点有运用顶点式求二次函数、一次函数的解析式、相似三角形的判定与性质、二次函数的性质综合性较强,正确利用相似三角形的判定与性质是解题关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
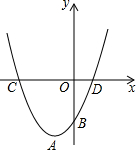 如图,已知抛物线y=ax2+2x+c的顶点为A(-1,-4),与y轴交于点B,与x轴负半轴交于点C.
如图,已知抛物线y=ax2+2x+c的顶点为A(-1,-4),与y轴交于点B,与x轴负半轴交于点C.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知抛物线y=ax2+x+c(a≠0)经过A(-1,0),B(2,0)两点,与y轴相交于点C.
已知抛物线y=ax2+x+c(a≠0)经过A(-1,0),B(2,0)两点,与y轴相交于点C. 查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
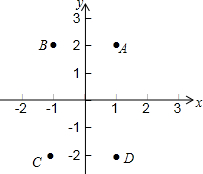 如图,平面内四个点的坐标分别为A(1,2),B(-1,2),C(-1,-2),D(1,-2),依次连接点A,B,C,D,则四边形ABCD的面积为( )
如图,平面内四个点的坐标分别为A(1,2),B(-1,2),C(-1,-2),D(1,-2),依次连接点A,B,C,D,则四边形ABCD的面积为( )| A. | 2 | B. | 4 | C. | 8 | D. | 16 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com